
What is the perimeter of a regular octagon with a radius of length 20?
Answer
436.2k+ views
Hint: Here in this question, we have to find the perimeter of a regular octagon of given radius of length
Complete step-by-step answer:
In geometry, perimeter can be defined as the path or the boundary that surrounds a shape. It can also be defined as the length of the outline of a shape.
If a octagon is regular, then all the sides are equal in length, and eight angles are of equal measures
Consider a regular octagon having radius of length
In figure, the red circle circumscribes the outer radius and the green circle the inner one.
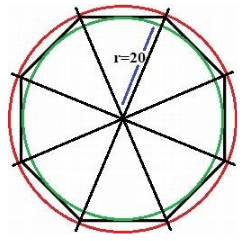
Let consider
Then, the vertices of the octagon centred at origin i.e.,
So the length of one side of regular octagon is distance between
Let consider a distance formula
Take
Simplify using a algebraic identity
On simplification, we get
Which is the length of the each side of the regular octagon when
Then perimeter of regular octagon is
On substituting equation (1), we have
given
On using calculator, we get the exact value
Now, consider
The inner radius will be
From the figure we have
By using a calculator, the value of
On cross multiplication, we have
On substituting equation (2) in (1), we get the length of each side i.e.,
To rationalize the denominator, we have to multiply and divide the RHS by
On simplification, we get
Which is the length of each side of the regular octagon when
Then perimeter of regular octagon is
On substituting equation (1), we have
given
On using calculator, we get the exact value
Hence, the perimeter of regular octagon of radius 20 is
If the outer radius is 20, then the perimeter is:
If the inner radius is 20, then the perimeter is:
So, the correct answer is “
Note: While determining the perimeter we use the formula. The unit for the perimeter will be the same as the unit of the length of a side or polygon. Whereas the unit for the area will be the square of the unit of the length of a polygon. We should not forget to write the unit with a final answer and we should also know about regular and irregular polygons.
Complete step-by-step answer:
In geometry, perimeter can be defined as the path or the boundary that surrounds a shape. It can also be defined as the length of the outline of a shape.
If a octagon is regular, then all the sides are equal in length, and eight angles are of equal measures
Consider a regular octagon having radius of length
In figure, the red circle circumscribes the outer radius and the green circle the inner one.

Let consider
Then, the vertices of the octagon centred at origin i.e.,
So the length of one side of regular octagon is distance between
Let consider a distance formula
Take
Simplify using a algebraic identity
On simplification, we get
Which is the length of the each side of the regular octagon when
Then perimeter of regular octagon is
On substituting equation (1), we have
given
On using calculator, we get the exact value
Now, consider
The inner radius will be
From the figure we have
By using a calculator, the value of
On cross multiplication, we have
On substituting equation (2) in (1), we get the length of each side i.e.,
To rationalize the denominator, we have to multiply and divide the RHS by
On simplification, we get
Which is the length of each side of the regular octagon when
Then perimeter of regular octagon is
On substituting equation (1), we have
given
On using calculator, we get the exact value
Hence, the perimeter of regular octagon of radius 20 is
If the outer radius is 20, then the perimeter is:
If the inner radius is 20, then the perimeter is:
So, the correct answer is “
Note: While determining the perimeter we use the formula. The unit for the perimeter will be the same as the unit of the length of a side or polygon. Whereas the unit for the area will be the square of the unit of the length of a polygon. We should not forget to write the unit with a final answer and we should also know about regular and irregular polygons.
Recently Updated Pages
Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Trending doubts
State and prove Bernoullis theorem class 11 physics CBSE

1 ton equals to A 100 kg B 1000 kg C 10 kg D 10000 class 11 physics CBSE

State the laws of reflection of light

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

1 Quintal is equal to a 110 kg b 10 kg c 100kg d 1000 class 11 physics CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells




