Question

What is the period of \[f\left( x \right) = 0.5\sin \left( x \right)\cos \left( x \right)\]?

Answer 1

Hint: A period of a function is basically the time interval between two waves in a graph. i.e. it is the interval or length after which the function repeats its graph. We will first simplify the given expression first and write it in simple form. After that, we know that, If \[T\] is the period of the function \[f(x)\], then the period of function \[c.f(ax + b)\] is given by \[\dfrac{T}{{|a|}}\]. We will simplify the expression given by using some of the trigonometric formulas. The formula we will use here is \[\sin \left( {2x} \right) = 2\sin \left( x \right)\cos \left( x \right)\].

Complete step by step solution:
We need to find the period of the function \[f\left( x \right) = 0.5\sin \left( x \right)\cos \left( x \right)\]
First, we need to simplify \[f\left( x \right) = 0.5\sin \left( x \right)\cos \left( x \right)\]
Changing decimal into fraction, we get
\[f\left( x \right) = \dfrac{5}{{10}}\sin \left( x \right)\cos \left( x \right)\]
After simplifying the fraction term, we get
\[ \Rightarrow f\left( x \right) = \dfrac{1}{2}\sin \left( x \right)\cos \left( x \right)\]
Now, in order to obtain the formula, we will multiply and divide the right hand side by \[2\].
\[ \Rightarrow f\left( x \right) = \dfrac{2}{2} \times \dfrac{1}{2}\sin \left( x \right)\cos \left( x \right)\]
Now, multiplying the numerators and denominators, we get
\[ \Rightarrow f\left( x \right) = \dfrac{{2\sin \left( x \right)\cos \left( x \right)}}{4}\]
Using \[\sin \left( {2x} \right) = 2\sin \left( x \right)\cos \left( x \right)\] in the numerator, we get
\[ \Rightarrow f\left( x \right) = \dfrac{{\sin \left( {2x} \right)}}{4}\]
\[ \Rightarrow f\left( x \right) = \dfrac{1}{4}\sin \left( {2x} \right)\]
Now, let us first see the period of \[\sin \left( x \right)\] through a graph.
Following is the graph of \[\sin \left( x \right)\].

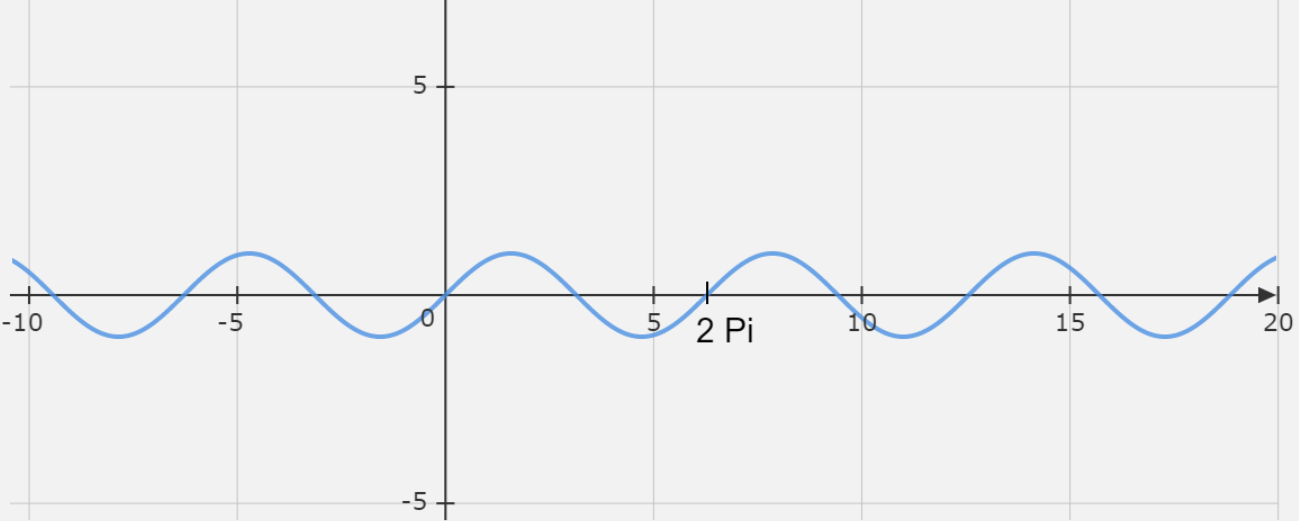
Here, we see that the graph repeats itself after a point and the point is \[2\pi \]. Hence, we can say that the period of \[\sin \left( x \right)\] is \[2\pi \].
Now, we have \[f\left( x \right) = \dfrac{1}{4}\sin \left( {2x} \right)\]
Let us consider \[\sin \left( x \right) = g\left( x \right)\]
Hence, our \[f\left( x \right)\] becomes \[f\left( x \right) = \dfrac{1}{4}g\left( {2x} \right) - - - - - - (1)\]
Comparing \[f\left( x \right) = \dfrac{1}{4}g\left( {2x} \right)\] with \[c.g\left( {ax + b} \right)\], we get
\[ \Rightarrow c = \dfrac{1}{4} - - - - - - (2)\]
\[ \Rightarrow a = 2 - - - - - - (3)\]
\[ \Rightarrow b = 0 - - - - - - (4)\]
Now, we know if \[T\] is the period of \[g\left( x \right)\], then \[\dfrac{T}{{|a|}}\] is the period of \[c.g\left( {ax + b} \right)\].
So, here we have period of \[g\left( x \right) = 2\pi \]
So, \[T = 2\pi - - - - - - (5)\]
Therefore, period of \[c.g\left( {ax + b} \right) = \dfrac{1}{4}g\left( {2x} \right)\] is given by \[\dfrac{T}{{|a|}}\]
Hence, Using (3) and (5) in the above formula, we get
Period of \[\dfrac{1}{4}g\left( {2x} \right) = \dfrac{{2\pi }}{{|2|}}\]
As we know, \[|2| = 2\], so
Period of \[\dfrac{1}{4}g\left( {2x} \right) = \dfrac{{2\pi }}{2}\]
After simplifying, we get
Period of \[\dfrac{1}{4}g\left( {2x} \right) = \pi - - - - - - (6)\]
Hence, by (1) and (6), we get
Period of \[f\left( x \right) = \pi \].
Hence, the period of \[f\left( x \right) = 0.5\sin \left( x \right)\cos \left( x \right)\] is \[\pi \].

Note:
We know that \[\alpha \] is said to be a period of the function \[f\left( x \right)\] if \[f\left( x \right) = f\left( {x + \alpha } \right)\]. So, we can get a countably infinite number of periods for a function. But in order to find the period of a function, we normally take the fundamental period of the function i.e. the smallest positive period of all the periods of the function. Also, we must know the period for all the basic trigonometric functions and remember that adding constant does not change the period of the function.