Question

What is the phase constant for SHM with $a(t)$ given in above figure, if the position function $x(t)$ has the form \[x = {x_m}cos\left( {\omega t + \phi } \right)\] and as \[\;{a_s} = 4.0m/{s^2}\] ?

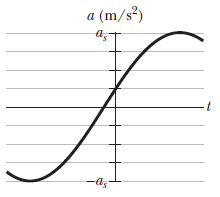
Answer 1

Hint: The position function for the sinusoidal wave can be equated as the function for the change in acceleration with time. By using the graph and plotting out the value of acceleration at time $t = 0$, we can use the acceleration function to determine the phase constant $\phi $.

Formulae used :
${a_m} = {\omega ^2}{x_m}$ where ${a_m}$ is the acceleration at position ${x_m}$ and $\omega $ is the angular frequency
\[x = {x_m}cos\left( {\omega t + \phi } \right)\] where $x$is its position at time $t$ , $\omega $ is the angular frequency and $\phi $ is the phase constant
\[a = - {\omega ^2}{x_m}cos\left( {\omega t + \phi } \right)\] where ${x_m}$is its position at time $t$ , $a$is the acceleration , $\omega $ is the angular frequency and $\phi $ is the phase constant.

Complete step by step solution:
The scale of the graph is given as ${a_s} = 4m/{s^2}$ .
So, by studying the graph, we can infer that at time $t = 0$,
${a_0} = 1m/{s^2}$
Now we know that ${a_m} = {\omega ^2}{x_m}$
By using the formula in our question, we get
${a_s} = {\omega ^2}{x_s} = 4m/{s^2}$
Therefore, using the formula \[a = - {\omega ^2}{x_m}cos\left( {\omega t + \phi } \right)\] to find the acceleration at time $t = 0$,
We get -
\[{a_0} = - {\omega ^2}{x_s}cos\left( {\omega t + \phi } \right)\]
\[
   \Rightarrow {a_0} = - {\omega ^2}{x_s}cos\left( {\omega t + \phi } \right) \\
   \Rightarrow \dfrac{{{a_0}}}{{ - {\omega ^2}{x_s}}} = cos\left( {\omega t + \phi } \right) \\
   \Rightarrow cos\left( {\omega t + \phi } \right) = \dfrac{{{a_0}}}{{ - {\omega ^2}{x_s}}} \\
   \Rightarrow \omega t + \phi = {\cos ^{ - 1}}\left( {\dfrac{{{a_0}}}{{ - {\omega ^2}{x_s}}}} \right) \\
    \\
 \]

Now, substituting the respective values at their respective places, we have -
\[
   \Rightarrow \omega \times 0 + \phi = {\cos ^{ - 1}}\left( {\dfrac{1}{{ - 4}}} \right) \\
   \Rightarrow \phi = {\cos ^{ - 1}}\left( {\dfrac{1}{{ - 4}}} \right) \\
 \]
The function \[{\cos ^{ - 1}}\left( {\dfrac{1}{{ - 4}}} \right)\] returns us with two possible values of $\phi $, which are $ + 1.82rad$
Or $ - 4.46rad$
The second value can be rejected as it gives a negative slope at time $t = 0$ and we could verify from the graph that the slope is positive at that specific time.

Note:
The phase constant \[\phi \] determines the initial position of the oscillation, that is, the position at $t = 0$. As \[\phi \] goes from $0$ to \[2\pi \], the initial position goes from the maximum amplitude to the minimum amplitude and back to the maximum amplitude, as the cosine of the phase.