Question

Plot a labeled graph of $\left| {{V_s}} \right|$where ${V_s}$ is stopping potential versus frequency f of the incident radiation.
State how you will use this graph to determine the value of Planck's constant.

Answer 1

Hint: In this question, we will first see the basic definition of stopping voltage and then further we will use the basic formulae of stopping potential and slope to get the required graph and the result. Further, we will see the basics of work function and Planck’s constant. We will also understand about the process of photoelectric effect, for our better understanding.

Formula used:
 ${V_s} = \dfrac{{hf}}{e} - \dfrac{\phi }{e}$
$Slope = e \times h$

Complete step by step solution:
As we know that the stopping potential or the cut-off potential can be defined as the potential that is required to stop the removal of an electron from a metal surface when the incident light energy or the radiation is greater than the work potential of the metal on which the incident light is focused.

Let us suppose that the work function of the metal is given by $\phi $
So, the stopping potential ${V_s}$​ will be given by:
${V_s} = \dfrac{{hf}}{e} - \dfrac{\phi }{e}$

So, we can observe that our graph of $\left| {{V_s}} \right|$ versus f will be a straight line, having the slope i.e., eh​ as shown in the figure below.

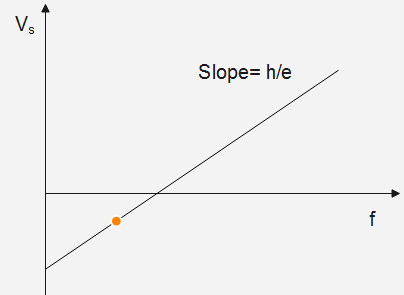
Now, when we find the slope from the observed graph, we can easily determine the value of Planck's constant, which is given by:
 $Slope = \dfrac{h}{e}$
$\therefore h = e \times Slope$
Therefore, we get the required result.

Additional information:
As we know that the stopping potential does not depend on the intensity of incident radiation. When we increase the intensity of the radiation, the value of saturated current increases, but the stopping potential of the metal remains unchanged.

We know that the work function is defined as the minimum thermodynamic work or we can call it energy, which is required to remove an electron from a solid usually metal to a given point in the vacuum immediately outside the solid surface or the metal surface.

Also, when electrons are emitted when electromagnetic radiation, such as light, hits the material or its surface is called the photoelectric effect. The work function for photoelectric effect is different for different materials. It depends upon the intensity of light. So, we know that the work function is the property of a material.

We also know that the Planck's constant is defined as the physical constant that gives relation between energy carried by a single photon and its corresponding frequency.

Note:
We should remember that, for a given intensity of radiation, the value of stopping potential of the metal depends on the frequency. We can say that, the higher the frequency of incident light or radiation, higher the value of the stopping potential of the metal. Also, the value of Planck’s constant is
$h = 6.626 \times {10^{ - 34}}{m^2}kg/s$.