Question

How do you plot the equation by plotting point \[x=2\]?

Answer 1

Hint: In this problem, we have to graph the given equation. We can see that the given equation is a straight-line equation. The equation \[x=2\] is a straight line, which is parallel to the y-axis and the line passes through all the points in the plane with an x-coordinate of 2.

Complete step by step answer:
We know that the given linear equation is \[x=2\].
We also know that the given equation is a straight line, which is parallel to the y-axis and the line passes through all the points in the plane with an x-coordinate of 2.
We should also know that the equation \[x=2\] represents a vertical line with only an x-intercept. This line will intersect the x-axis at 2.
We can also plot some points, through which the line passes through.
If we want to plot the points, we will have points where x value is always 2, regardless of the value for y.
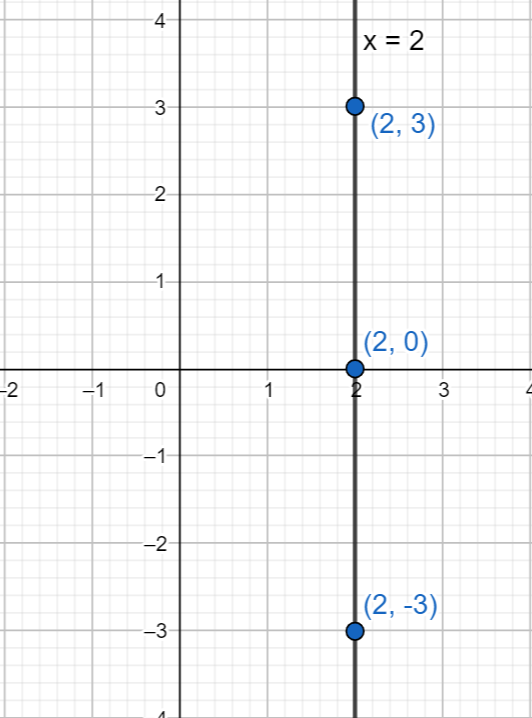
We can see that the points \[\left( 2,-3 \right)\left( 2,0 \right)\left( 2,3 \right)\] which is on the line \[x=2\].
Now we can graph the given line \[x=2\] and some points through which the line passes.

Note: Students make mistakes in understanding the concept of line equation. We should know that to solve these types of problems, we have to understand the concept of line. We should also know that the equation represents a vertical line with only an x-intercept. This line will intersect the x-axis at the point given.