Question

PNP’ is the double ordinate of the parabola. Prove that the locus of the point of intersection of the normal at \[P\] and the diameter through \[{{P}^{'}}\] is equal to the parabola \[{{y}^{2}}=4a\left( x-4a \right)\].

Answer 1

Hint: The equation of diameter is given as \[y=\dfrac{2a}{m}\] , where \[m\] is the slope of the diameter.

 A double ordinate is a chord which is perpendicular to the axis of the parabola .
 Let the equation of the parabola be \[{{y}^{2}}=4ax\].

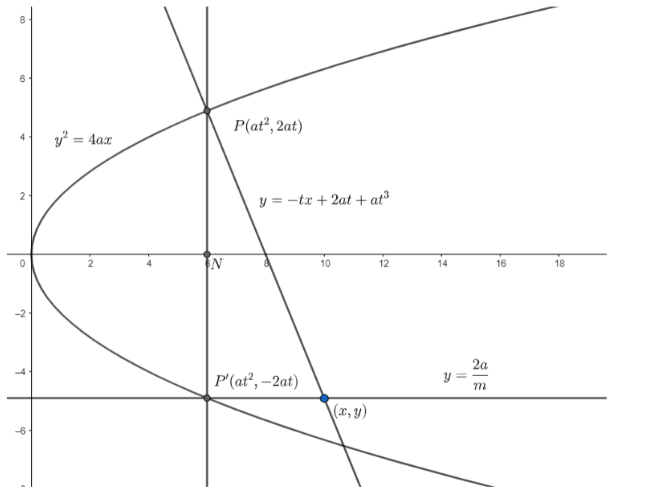
First , we need to find the equation of normal at \[P\].
We know the parametric coordinates of any point on the parabola can be written as \[P\left( a{{t}^{2}},2at \right)\].
Now , we know that a double ordinate is a chord which is perpendicular to the axis of the parabola .
So , the double ordinate of the point \[P\left( a{{t}^{2}},2at \right)\] will be \[{{P}^{'}}\left( a{{t}^{2}},-2at \right)\].
Now , we will find the equation of normal at \[P\].
We know, the equation of normal at \[\left( a{{t}^{2}},2at \right)\] is given as \[y=-tx+2at+a{{t}^{3}}\]
So , the equation of normal at \[P\] is given as \[y=-tx+2at+a{{t}^{3}}....\left( i \right)\]
Now, we will find the equation of diameter at \[{{P}^{'}}\].
We know, the general equation of diameter is given as \[y=\dfrac{2a}{m}.....(ii)\], where \[m\] is the slope of the diameter.
Now , we will find the point of intersection of the normal and the diameter . Let this point be \[(x,y)\] .
In the question , it is given that the diameter passes through \[{{P}^{'}}\].
So , we will substitute \[y=-2at\] in equation \[(ii)\].
On substituting \[y=-2at\] in \[y=\dfrac{2a}{m}\], we get
\[-2at=\dfrac{2a}{m}\]
\[\Rightarrow m=\dfrac{-1}{t}\]
Now, we will substitute \[m=\dfrac{-1}{t}\] in \[(ii)\]. So, we get,
On substituting \[m=\dfrac{-1}{t}\] in \[(ii)\], we get,
\[y=-2at.....\left( iii \right)\]
Substituting \[y=-2at\] in \[\left( i \right)\], we get
\[-2at=-tx+2at+a{{t}^{3}}\]
Or, \[tx=4at+a{{t}^{3}}\]
Or, \[x=4a+a{{t}^{2}}....\left( iv \right)\]
Now , from \[\left( iii \right)\], we have
\[t=\dfrac{-y}{2a}\]
Now , we will substitute \[t=\dfrac{-y}{2a}\] in equation \[\left( iv \right)\].
On substituting \[t=\dfrac{-y}{2a}\] in equation \[\left( iv \right)\], we get
\[x=4a+a{{\left( \dfrac{-y}{2a} \right)}^{2}}\]
\[\Rightarrow x-4a=\dfrac{{{y}^{2}}}{4a}\]
\[\Rightarrow {{y}^{2}}=4a\left( x-4a \right)\]
Hence , the locus of the point of intersection of the normal at \[P\] and the diameter through \[{{P}^{'}}\] is equal to the parabola \[{{y}^{2}}=4a\left( x-4a \right)\].

Note: While substituting the values of \[m\] and \[t\], make sure the signs are correct. Students generally get confused in signs and make a mistake.