Question

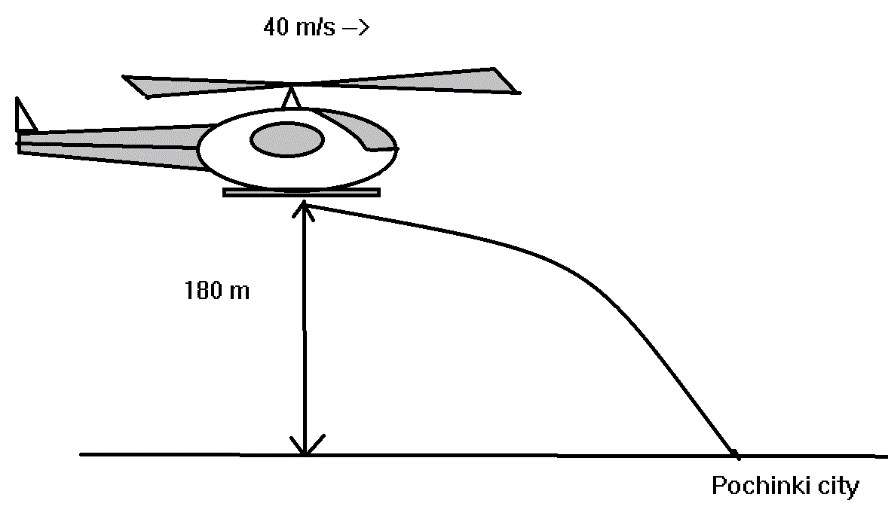
Pochinki, a city in the Erangel map in PUBG, is one of the deadliest places to drop. A novice player, in lure maximum loot, aims to have a drop at Pochinki is released from a helicopter flying horizontally at a constant velocity $40m{s^{ - 1}}$. How far from the city of Pochinki (in km), horizontally, the player needs to drop if the helicopter is flying at a height of $180m$from the ground. $[g = 10m{s^{ - 2}}]$

Answer 1

Hint Such type of question can be solved by using Newton’s law of motion. Using this equation we first find the time to fall by loot to reach the ground when it is released from the helicopter by using the height of the helicopter from the ground and gravitational acceleration. Now by using that time we will find how far the loot will be dropped when released from the helicopter.
Formula used:
Newton’s law of motion
$ \Rightarrow d = ut + \dfrac{1}{2}a{t^2}$
Formula of speed
$ \Rightarrow v = \dfrac{d}{t}$

Complete Step by step solution
As the helicopter is moving with speed $40m/s$and it is $180m$ above the ground. So using Newton’s law of motion which gives the relation between acceleration, time, and distance along the y-axis.
$ \Rightarrow {d_y} = {u_y}t + \dfrac{1}{2}g{t^2}$ ----------------- Equation $(1)$
As given${d_y} = 180m$, also ${u_y} = 0$ as the helicopter is moving along the x-axis, gravitational acceleration$g = 10m{s^{ - 2}}$. Substituting all these quantities in the equation$(1)$we get
$ \Rightarrow 180 = 0 + \dfrac{1}{2} \times 10 \times {t^2}$
$ \Rightarrow {t^2} = 180 \times 2 \times \dfrac{1}{{10}}$
Hence the time of fall will be given as solving the above equation
$ \Rightarrow t = \sqrt {36} $
$\therefore t = 6s$
Now we will find the distance at which loot will drop after it is released from the helicopter. As this motion is along the x-axis the formula of speed can be given along the x-axis as
$ \Rightarrow {s_x} = \dfrac{{{d_x}}}{t}$
$ \Rightarrow {d_x} = {s_x} \times t$ --------------------- Equation $(2)$
As given ${s_x} = 40m/s$and we get$t = 6s$. So substituting them in the Equation $(2)$ we get
$ \Rightarrow {d_x} = 40m/s \times 6s$
$\therefore {d_x} = 240m = 0.240km$
Therefore the distance at which the loot will drop after it is released by moving helicopter

with the speed of $40m/s$and $180m$above the ground will be at $0.240km$.

Note When we are dealing with such questions we have to stay aware of the equations of motion and also we have to consider the axis of motion in which the object is moving. In this question, the helicopter is moving parallel with the x-axis.