Question

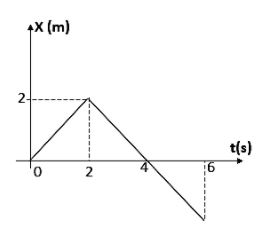
Position-time graph of a particle of mass $ 2Kg $ is shown in figure. Total work done on the particle from $ t=0 $ to $ t=4s $ is

Answer 1

Hint: The position time graph is given. From this graph, we can find out the velocity of the particle by taking the derivative or the slope from the graph. After this find out the force acting on each interval. Then find out the work done using the force.

Complete step-by-step answer:
 from the graph we can see that this is a position time graph. We can divide the distance travelled in two intervals,
 $ t=0 \ to \ t=2s $
And $ t=2s\ to \ t=4s $
Let us consider the first interval,
In this interval the velocity of the particle can be found out by the equation,
 $ v=\dfrac{{{x}_{2}}-{{x}_{1}}}{{{t}_{2}}-{{t}_{1}}} $
Where \[{{x}_{2}}\]be the second position on the y-axis,\[{{x}_{1}}\]is the first position on y-axis,\[{{t}_{2}}\]is the time at which body is in second position and \[{{t}_{1}}\]is the time at which body is in first position.
Substituting the values in it,
 $ v=\dfrac{2-0}{2-0}=1 $
Therefore the velocity is given as
 $ v=1m{{s}^{-1}} $
 In the next interval, let us find the velocity of particle,
 $ v=\dfrac{{{x}_{2}}-{{x}_{1}}}{{{t}_{2}}-{{t}_{1}}} $
Substituting the values in the second interval will give,
\[v=\dfrac{2-4}{4-2}=-1m{{s}^{-1}}\]
Therefore from this we can conclude that the velocity is a constant.
Now let us look at the acceleration. It is given by the equation,
\[a=\dfrac{dv}{dt}\]
As velocity is a constant, the acceleration will also be a constant.
The force on the body will be given as,
\[F=ma\]
Where\[m\]the mass of a particle, \[a\]is the acceleration of the particle. As the acceleration is zero, the force acting on the body will also be zero.
\[F=0N\]
And also we know that,
\[W=F\cdot S\]
\[F\]Is the force of the body and \[S\]is the displacement of the body. Since the force acting over the body is zero as we calculated, the work done will be zero.
\[W=0J\]
Therefore the answer is zero joule.

Note: Work done on a body is given as the increase in the energy of the body. If the applied force is in the opposite direction to the motion of the object, the work done is said to be negative. This means that energy is taken away from the body.