Question

Positive charge $Q$ is distributed uniformly over a circular ring of radius $R$. A particle having mass $m$ and a negative charge $q$ is placed on its axis at a distance $x$ from the centre. Find the force on the particle. Assuming $x << R$, find the time period of oscillation of the particle if it is released from there.

Answer 1

Hint: We know that the electric force is force experience due multiple charges, and is given by Coulomb's force. It states that the electric force depends on the charge q and inversely proportional to the square of the distance between them. We can use the above to solve the given problem..
Formula: $F=k\dfrac{q_{1}q_{2}}{r^{2}}$

Complete answer:
We know that the electric force is the force experienced due to a pair charges is given by Coulomb's force. Clearly, the electrical force between the charges, depends on the individual charge q and is inversely proportional to the square of the distance between them.
We know that, the electrical force $F$ between two charges $q_{1}$ and $q_{2}$ which is separated at a distance $r$ is given as $F=k\dfrac{q_{1}q_{2}}{r^{2}}$, where $k=\dfrac{1}{4\pi\epsilon_{0}}$ which is constant with a value $9\times 10^{9}$.
Similarly, an electric field E is defined as the electric force F per unit positive charge q, which is infinitesimally small and at rest, and is given as $E=\dfrac{F}{q}$. Then $E=\dfrac{kq}{r^{2}}$.
Here, given that the $-q$ is kept at a point, say, P at the axial point, at a distance $x$ from the ring.

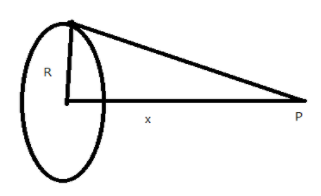
We know that the electric field due to a circular ring, of radius $R$ and charge $Q$ i is given as $E=\dfrac{kQx}{(R^{2}+x^{2})^{\dfrac{3}{2}}}$
$\implies E=\dfrac{kQx}{R^{3}}$
Then the force at P is given as, $F=qE=\dfrac{kQqx}{R^{3}}$
Let the amplitude of the electric field be $x$, then the time period of the electric field is given as
$T=2\pi\sqrt{\dfrac{x}{\dfrac{kQqx}{mR^{3}}}}$
$\implies T=2\pi\sqrt{\dfrac{mR^{3}x}{kQqx}}$
$\implies T=2\pi\sqrt{\dfrac{4\pi\epsilon_{0}mR^{3}}{Qq}}$
$\therefore T=\sqrt{\dfrac{16\pi^{2}\epsilon_{0}mR^{3}}{Qq}}$ is the time period of the electric field.

Note:
We know that the electric force due to a pair of charges is given by Coulomb's law. This force can be attractive or repelling depending on the nature of the charges. Electric field is in the direction of the force. However, the electric field also depends on the symmetry of the charge carrying conductor.