Question

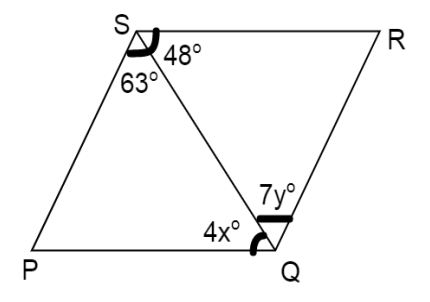
PQRS is a parallelogram. From the information given in the figure, find the values of $x$ and $y$.

Answer 1

Hint: We can solve this problem by using properties of angles of triangle and parallelogram. Since the diagonal is drawn, it is divided into two triangles. Also, these two triangles are congruent. Angle sum of a triangle and relation between opposite angles of a parallelogram are known.

Useful formula:
Sum of angles of a triangle is \[{180^ \circ }\].
Opposite angles of a parallelogram are equal.

Complete step by step solution:
Given a parallelogram with one of the diagonals drawn. So, we have two triangles here, $\Delta PQS$ and $\Delta SQR$.
Sum of angles of a triangle is \[{180^ \circ }\].
Consider $\Delta PQS$
we have, $\angle P + \angle PQS + \angle QSP = {180^ \circ }$
$ \Rightarrow \angle P + 4x + {63^ \circ } = {180^ \circ }$
Simplifying we get,
$ \Rightarrow \angle P + 4x = {180^ \circ } - {63^ \circ }$
$ \Rightarrow \angle P + 4x = {117^ \circ } - - - (i)$
Similarly consider $\Delta SQR$,
$\angle RSQ + SQR + QRS = {180^ \circ }$
Substituting we get,
$ \Rightarrow {48^ \circ } + 7y + \angle R = {180^ \circ }$
Simplifying we get,
$ \Rightarrow 7y + \angle R = {180^ \circ } - {48^ \circ }$
$ \Rightarrow 7y + \angle R = {132^ \circ } - - - (ii)$
Opposite angles of a parallelogram are equal.
$ \Rightarrow \angle P = \angle R = k(say)$
$(i) \Rightarrow k + 4x = {117^ \circ }$
$(ii) \Rightarrow 7y + k = {132^ \circ }$
Adding these two equations we get,
$k + 4x + 7y + k = {117^ \circ } + {132^ \circ }$
$ \Rightarrow 4x + 7y + 2k = {249^ \circ } - - - (iii)$
Also, $\angle Q = \angle S \Rightarrow 4x + 7y = {63^ \circ } + {48^ \circ }$
$ \Rightarrow 4x + 7y = {111^ \circ } - - - (iv)$
Comparing $(iii)$ and $(iv)$ we get,
$2k = {249^ \circ } - {111^ \circ } = {138^ \circ }$
Dividing by $2$ we have,
$ \Rightarrow k = \dfrac{{138}}{2} = {69^ \circ }$
Therefore, $\angle P = \angle R = {69^ \circ }$
So, from $(i),4x = {117^ \circ } - \angle P = 117^\circ - 69^\circ = 48^\circ $
$ \Rightarrow x = \dfrac{{48^\circ }}{4} = 12^\circ $
Also, from $(ii),7y = 132^\circ - 69^\circ = 63^\circ $
$ \Rightarrow y = \dfrac{{{{63}^ \circ }}}{7} = {9^ \circ }$
$\therefore x = {12^ \circ },y = {9^ \circ }$

Additional information:
For any polygon with $n$ sides,
Sum of interior angles is equal to $(n - 2){90^ \circ }$.
Sum of exterior angles is equal to ${360^ \circ }$.

Note:Here we used two properties to establish the relation between the given angles. Sum of angles of a triangle is \[{180^ \circ }\] and opposite angles of a parallelogram are equal. Also, we have other facts as well. Sum of angles of a parallelogram (actually any quadrilateral) is ${360^ \circ }$. And also, adjacent angles of a parallelogram are supplementary (that is angle sum is equal to ${180^ \circ }$). We can consider any of these properties individually or combined to solve this question.