
PQRS is a square. If
A).
B).
C).
D).
Answer
424.5k+ views
Hint: The length of one side of a square is given. We know that all four sides of a square will have the same length. Here we have to find the diagonal of the square. A diagonal of a square can split the square into two right-angled triangles where the diagonal will be the hypotenuse so using the Pythagoras theorem, we can find the length of the diagonal.
Formula:
Pythagoras theorem:
And some other formulas that we need to know:
1.
2.
3.
Complete step-by-step solution:
It is given that
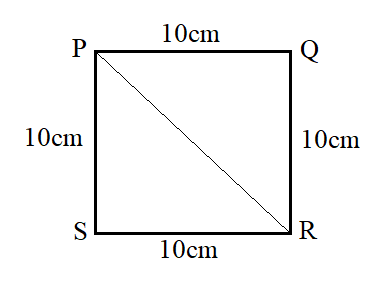
Therefore
We aim to find the length of
By Pythagoras theorem, we know that for a right-angled triangle
So, for the right-angled triangle
We know that
Substituting these values in
Simplifying this we get
On simplifying this we get
But we need the value for
Now let us write
Now let us write
Let us split the square root using the formula,
Noe using the formula
Again, using the formula
Therefore, the length of the diagonal of the square
Now let us see the options, option (a)
Option (b)
Option (c)
Option (d)
Thus, option (c)
Note: We can also take another right-angled triangle that is
Formula:
Pythagoras theorem:
And some other formulas that we need to know:
1.
2.
3.
Complete step-by-step solution:
It is given that

Therefore
We aim to find the length of
By Pythagoras theorem, we know that for a right-angled triangle
So, for the right-angled triangle
We know that
Substituting these values in
Simplifying this we get
On simplifying this we get
But we need the value for
Now let us write
Now let us write
Let us split the square root using the formula,
Noe using the formula
Again, using the formula
Therefore, the length of the diagonal of the square
Now let us see the options, option (a)
Option (b)
Option (c)
Option (d)
Thus, option (c)
Note: We can also take another right-angled triangle that is
Recently Updated Pages
Master Class 12 Economics: Engaging Questions & Answers for Success

Master Class 12 Maths: Engaging Questions & Answers for Success

Master Class 12 Biology: Engaging Questions & Answers for Success

Master Class 12 Physics: Engaging Questions & Answers for Success

Master Class 4 Maths: Engaging Questions & Answers for Success

Master Class 4 English: Engaging Questions & Answers for Success

Trending doubts
Full Form of IASDMIPSIFSIRSPOLICE class 7 social science CBSE

The southernmost point of the Indian mainland is known class 7 social studies CBSE

Convert 200 Million dollars in rupees class 7 maths CBSE

How many crores make 10 million class 7 maths CBSE

Write a pair of integers whose sum gives i Zero ii class 7 maths CBSE

List of coprime numbers from 1 to 100 class 7 maths CBSE





