
Pressure is a scalar quantity because
A. It is the ratio of force to area and both force and area are vectors.
B. It is the ratio of the magnitude of the force to area.
C. It is the ratio of the component of the force normal to the area.
D. It depends on the size of the area chosen.
Answer
573.9k+ views
Hint:The physical quantity can be referred to as the scalar quantity if it has only a magnitude and cannot be expressed by its direction. On the other hand, the physical quantity is said to be vector quantity if it has both magnitude and direction. The pressure is the ratio of force and area of cross-section on which the force is acting.
Complete answer:
Let’s recall the definition of scalar quantity and vector quantity. The physical quantity can be referred to as the scalar quantity if it has only a magnitude and cannot be expressed by its direction. On the other hand, the physical quantity is said to be vector quantity if it has both magnitude and direction.
We have the definition of pressure: The pressure is the ratio of force acting on the body per unit area of the body.
Therefore,
\[P = \dfrac{{\vec F}}{{\vec A}}\]
Thus, in the above equation we see both force and area vector are vector quantities and still the pressure is the scalar quantity. Let’s answer this using the fact that the pressure is the measure of force acting on the body normal to its area vector. Therefore, the pressure is always defined as the component of the force perpendicular to the area of cross-section of the body.
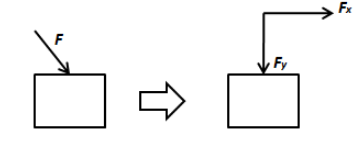
In the above figure, we can see the force F is acting on the block as shown in the figure. The pressure is measure of only the vertical component of the force. Thus, to determine the pressure, we don’t need to determine the direction of the original force F but the magnitude of the component of the force would be sufficient. Therefore, the correct answer is option (C).
If the applied force is not normal to the plane of the area of the cross section of the body, we cannot take its magnitude to determine the pressure. Therefore, the option (B) is incorrect.
The pressure depends on the size of the area chosen as well as the component of the force normal to the area chosen. Therefore, the option (D) is incorrect.
So, the correct answer is option (C).
Note:Sometimes students think that the pressure is the ratio of force and area and both force and area are vector quantities. Therefore, the pressure is scalar quantity because it is the ratio of two vector quantities. It is a false concept. Remember, the horizontal component of the force plays no role in resultant pressure in the above figure.
Complete answer:
Let’s recall the definition of scalar quantity and vector quantity. The physical quantity can be referred to as the scalar quantity if it has only a magnitude and cannot be expressed by its direction. On the other hand, the physical quantity is said to be vector quantity if it has both magnitude and direction.
We have the definition of pressure: The pressure is the ratio of force acting on the body per unit area of the body.
Therefore,
\[P = \dfrac{{\vec F}}{{\vec A}}\]
Thus, in the above equation we see both force and area vector are vector quantities and still the pressure is the scalar quantity. Let’s answer this using the fact that the pressure is the measure of force acting on the body normal to its area vector. Therefore, the pressure is always defined as the component of the force perpendicular to the area of cross-section of the body.

In the above figure, we can see the force F is acting on the block as shown in the figure. The pressure is measure of only the vertical component of the force. Thus, to determine the pressure, we don’t need to determine the direction of the original force F but the magnitude of the component of the force would be sufficient. Therefore, the correct answer is option (C).
If the applied force is not normal to the plane of the area of the cross section of the body, we cannot take its magnitude to determine the pressure. Therefore, the option (B) is incorrect.
The pressure depends on the size of the area chosen as well as the component of the force normal to the area chosen. Therefore, the option (D) is incorrect.
So, the correct answer is option (C).
Note:Sometimes students think that the pressure is the ratio of force and area and both force and area are vector quantities. Therefore, the pressure is scalar quantity because it is the ratio of two vector quantities. It is a false concept. Remember, the horizontal component of the force plays no role in resultant pressure in the above figure.
Recently Updated Pages
Master Class 9 General Knowledge: Engaging Questions & Answers for Success

Master Class 9 Social Science: Engaging Questions & Answers for Success

Master Class 9 English: Engaging Questions & Answers for Success

Master Class 9 Maths: Engaging Questions & Answers for Success

Master Class 9 Science: Engaging Questions & Answers for Success

Class 9 Question and Answer - Your Ultimate Solutions Guide

Trending doubts
Difference Between Plant Cell and Animal Cell

Fill the blanks with the suitable prepositions 1 The class 9 english CBSE

Who is eligible for RTE class 9 social science CBSE

Which places in India experience sunrise first and class 9 social science CBSE

What is pollution? How many types of pollution? Define it

Name 10 Living and Non living things class 9 biology CBSE




