Question

What is the prime factorization of \[364\]?

Answer 1

Hint: Prime factorization means expressing or writing the same number in the form of a product of prime numbers only. This method is generally used to find the LCM of two numbers. In this question, we need to find express \[364\] as the product of its prime factors. Here, we will determine the factors of \[364\] and then we will determine the prime factors of \[364\], using the method of prime factorization.

Complete step by step answer:
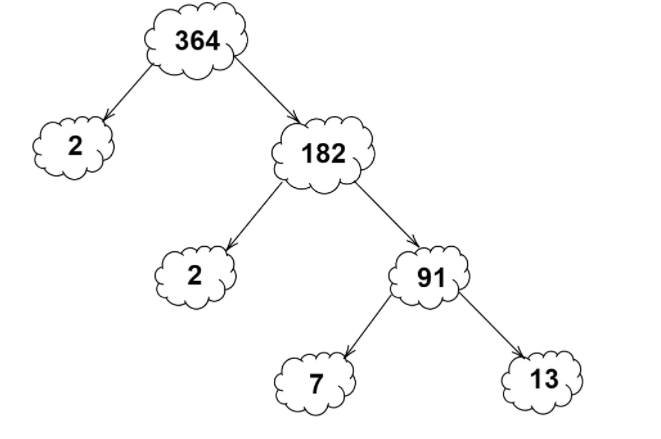
Here, we need to find the prime factors of \[364\] using prime factorization.We know that \[364\] is a composite number.Therefore, the possible factors of \[364\] are: $182 \times 2$, $91 \times 4$, $13 \times 28$, $7 \times 52$, $26 \times 14$, $1 \times 364$.

Prime factorization is a method of finding prime numbers which multiply to make the original number.A prime number is a natural number greater than $1$ that is not a product of two smaller natural numbers.In prime factorization, we start dividing the number by the first prime number $2$ and continue to divide by $2$ until we get a decimal or remainder. Then divide by $3,5,7,....$etc. until we get the remainder $1$ with the factors as prime numbers. Then write the numbers as a product of prime numbers.

So, we first divide the number by two. So, we get,
$364 = 2 \times 182$
We know that $182$ is still even. So, we can divide by two. Hence, we get,
$364 = 2 \times 2 \times 91$
Now, we know that $91 = 13 \times 7$. So, we get,
$364 = 2 \times 2 \times 7 \times 13$
Now, we know that all the numbers in the product are prime.
Thus, prime factorization of \[364\] is,
$364 = 2 \times 2 \times 7 \times 13$
This can be also written in exponential form as $364 = {2^2} \times {7^1} \times {13^1}$. But as all the prime factors appear only once in the prime factorisation of $364$.

Hence, the prime factorisation of $364$ is ${2^2} \times {7^1} \times {13^1}$.

Note: In this question it is important to note here that a composite number is a positive integer that can be formed by multiplying two smaller positive integers. Equivalently, it is a positive integer that has at least one divisor other than $1$ and itself. However, the prime factorization is also known as prime decomposition. And, the prime factorization of the prime number is the number itself and $1$. Every other number can be broken down into prime number factors, but the prime numbers are the basic building blocks of all the numbers. We also can use a vertical tabular form to express the same product.