Question

Proof the pascal’s law.

Answer 1

- Hint: Pascal’s law states that in a closed container if the fluid is in a rest condition (not moving) then a pressure change in one part of the container is transmitted to every part of the fluid and to the wall. In this phenomenon there is no loss of the fluid. In this principle the condition is that the gravity is neglected.

Complete step-by-step answer:
Statement- The intensity of pressure at a point in a fluid at rest is the same in all directions. (neglecting the effect of gravity)
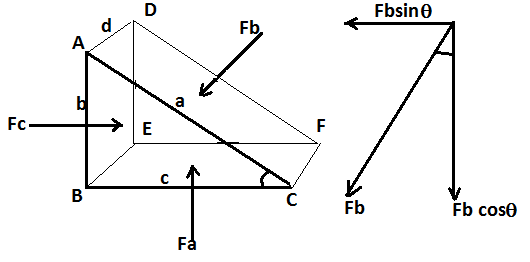
Proof:
Here from the above diagram let us assume that the $ {{ad,bd}} $ and $ {{cd}} $ are the areas of the faces ADFC,ADEB and BEFC.
And the forces acting on the faces of the triangular block are $ {{{F}}_{{{a,}}}}{{{F}}_{{b}}} $ and $ {{{F}}_{{c}}} $ , similarly let the pressure acting on the three faces $ {{{P}}_{1,}}{{{P}}_2} $ and $ {{{P}}_3} $ respectively.
We know that pressure is equal to the force divided by the area.
Mathematically,
 $ {{P = }}\dfrac{{{F}}}{{{A}}} $
So, from the above equation we can write the formula for the pressure force, that is,
 $ F = P \times A $
All the three pressures will exert a force on their respective faces normal to the surface.
Therefore, force $ {{{F}}_{{{a,}}}}{{{F}}_{{b}}} $ and $ {{{F}}_{{c}}} $ is given as:
 $ {{{F}}_{{a}}}{{ = }}{{{P}}_{{1}}}\times $ area of BEFC $ {{ = }}{{{P}}_{{1}}}\times cd $
 $ {{{F}}_{{b}}}{{ = }}{{{P}}_2} \times $ area of ADFC $ {{ = }}{{{P}}_2}\times ad $
 $ {{{F}}_{{c}}}{{ = }}{{{P}}_3}\times $ area of ADEB $ {{ = }}{{{P}}_3} \times bd $
In the above diagram let angle BAC= $ {{\theta }} $ ,
So now in the $ {{\Delta BAC}} $ ,
 $ {{sin\theta = }}\dfrac{{{b}}}{{{a}}} $ and $ {{cos\theta = }}\dfrac{{{c}}}{{{a}}} $
Since the above triangular block is in equilibrium then the net force on it will be zero.
So, balancing the forces for the triangular block to be in equilibrium,
 $ {{{F}}_{{a}}}{{ = }}{{{F}}_{{b}}}{{cos\theta }} $ ----equation (1)
and \[{{{F}}_{{b}}}{{sin\theta = }}{{{F}}_{{c}}}\]-----equation (2)
On putting the values of $ {{sin\theta }} $ and $ {{cos\theta }} $ value of the forces in the equation(1) and equation (2), we will get the relation as follows,
For equation (1),
 $ {P_{1}} \times cd = {P_{2}} \times ad \times \dfrac{c}{{a}} $
 $ {P_{1}}\times cd = {P_{2}} \times cd $
 $ {P_{1}} = {P_{2}} $ --------equation (3)
Similarly, for equation (2)
 $ {{{P}}_{{2}}}{{ \times ad \times }}\dfrac{{{b}}}{{{a}}} = {{{P}}_3}{{ \times bd}} $
 $ {{{P}}_{{2}}}{{ \times bd}} = {{{P}}_3}{{ \times bd}} $
  $ {{{P}}_{{2}}} = {{{P}}_3} $ ---------equation (4)
Now from equation (3) and equation (4), we see that $ {{{P}}_{{1}}}{{ = }}{{{P}}_{{2}}} $ and $ {{{P}}_{{2}}} = {{{P}}_3} $ , so this implies that all the values of the pressure are mutually equal to each other.
So, $ {{{P}}_1}{{ = }}{{{P}}_{{2}}} = {{{P}}_3} $
Hence proved.

Note: Applications of the pascal’s law are very useful in our day to day life and in some other industrial applications. Pascal’s law is used in:
Force amplification in braking systems of many vehicles
Hydraulic press.
Automatic lift (hydraulic jack) at many service stations.
Artesian wells
Water towers and
Dams, etc.