Question

How do you prove Ptolemy's Theorem that in a cyclic quadrilateral, the sum of the products of opposite pairs of sides is equal to the product of the diagonals?
In cyclic quadrilateral ABCD, \[AB \times CD + BC \times AD = AC \times BD\].

Answer 1

Hint: To prove the Ptolemy's Theorem, draw a cyclic quadrilateral ABCD, in which AC and BD are its diagonals which intersect at P. Considering its respective angles and triangles whose corresponding sides are proportional. Hence, by this we can prove the theorem.

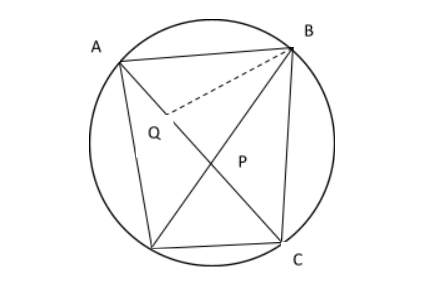
Complete step by step answer:
Ptolemy's Theorem states that in a cyclic quadrilateral, the sum of the products of opposite pairs of sides is equal to the product of the diagonals.
In the figure, ABCD is the cyclic quadrilateral inscribed in a circle as described below. Let us also join its diagonals AC and BD to intersect at P.
To prove that \[AB \times CD + BC \times AD = AC \times BD\], let us draw an angle
\[\angle ABQ = \angle CBD\] to intersect AC at Q as shown in the figure.
In \[\Delta ABQ\]and \[\Delta CBD\], we have
By construction we have
\[\angle ABQ = \angle CBD\]
Angles in the same arc we have
\[\angle BAQ = \angle CDB\]
Therefore,
\[\Delta ABQ \sim \Delta CBD\]
As we can see in the adjoining figure that both the obtained triangles are almost similar, hence the corresponding sides are proportional to each other
\[\dfrac{{AB}}{{BD}} = \dfrac{{AQ}}{{CD}}\]
Simplifying the terms, we get
\[AB \times CD = BD \times AQ\] ……………….. 1
Similarly, as \[\angle ABQ = \angle CBD\] we have
\[\angle ABQ + \angle QBP = \angle CBD + \angle QBP\]
 And in \[\Delta ABD\]and \[\Delta QBC\], we have angles in the same arc AB as
\[\angle ABD = \angle QBC\]
\[\angle ADB = \angle QCB\]
Hence, this implies that
\[\Delta ABD \sim \Delta QBC\]
As we can see in the adjoining figure that both the obtained triangles are almost similar, hence the corresponding sides are proportional to each other
\[\dfrac{{AD}}{{QC}} = \dfrac{{BD}}{{BC}}\]
Simplifying the terms, we get
\[AD \times BC = BD \times QC\] ……………….. 2
Adding equation 1 and 2, we get
Equation 1 is
\[AB \times CD = BD \times AQ\]
Equation 2 is
\[AD \times BC = BD \times QC\]
Simplifying we get
\[AB \times CD + BC \times AD = \left( {AQ + QC} \right) \times BD\]
\[AB \times CD + BC \times AD = AC \times BD\]

Note: To prove Ptolemy's Theorem as it is a relation between the four sides and two diagonals of a cyclic quadrilateral, considering its respective angles and triangles whose corresponding sides are proportional we can prove the theorem. In a quadrilateral, if the sum of the products of the lengths of its two pairs of opposite sides is equal to the product of the lengths of its diagonals, then the quadrilateral can be inscribed in a circle i.e., it is a cyclic quadrilateral.