Question

Prove that a cyclic rhombus is a square.

Answer 1

Hint: The quadrilateral having all sides of equal length is called rhombus. A square has all sides equal and also all interior angles are right angles. Any rhombus is a square if any angle of the rhombus is the right angle.

Complete step by step answer:
Consider a rhombus \[PQRS\] inside of a circle as shown below.

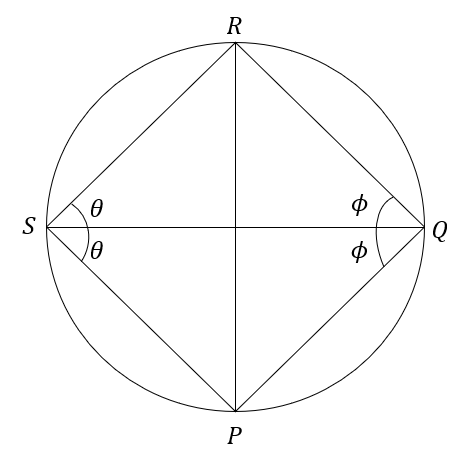
In the above figure, the diagonal \[SQ\] is the angular bisector of angle \[S\] and angle \[Q\].
In \[\Delta PQS\] and \[\Delta QRS\],
\[
  \,\,\,\,\,\,PS = QR,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( {{\text{sides of rhombus are equal}}} \right) \\
   \Rightarrow PQ = RS,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( {{\text{sides of rhombus are equal}}} \right) \\
   \Rightarrow SQ = SQ\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( {{\text{common side}}} \right) \\
\]
Thus, \[\Delta PQS \cong \Delta QRS\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( {{\text{SSS congruence}}} \right) \]
Since, the opposite angles of a cyclic quadrilateral are always supplementary, it can be written as follows:
\[
  \,\,\,\,\,\,2\theta + 2\phi = 180^\circ \\
   \Rightarrow 2\left( {\theta + \phi } \right) = 180^\circ \\
   \Rightarrow \theta + \phi = \dfrac{{180^\circ }}{2} \\
   \Rightarrow \theta + \phi = 90^\circ \\
\]
In \[\Delta PQS\],
\[
  \,\,\,\,\,\,\theta + \phi + \angle P = 180^\circ \\
   \Rightarrow 90^\circ + \angle P = 180^\circ \\
   \Rightarrow \angle P = 180^\circ - 90^\circ \\
   \Rightarrow \angle P = 90^\circ \\
\]

Since, an angle of the rhombus \[PQRS\] is right angle, the rhombus \[PQRS\] is a square.

Note: Any rhombus is said to be a square if any angle of the rhombus is the right angle. A quadrilateral is said to be square, if all the sides of the quadrilateral are equal and every angle is a right angle. The angle formed inside of a semicircle is the right angle.