Question

Prove that a cyclic trapezium is isosceles and its diagonals are equal.

Answer 1

Hint: First we will draw the required trapezium ABCD and then we will draw a parallel line CE to AD. Then we will use that parallelogram AECD to prove that the cyclic quadrilateral is isosceles. Now we will use the SAS rule of congruence to prove that the diagonals AC and BD are equal.

Complete step-by-step solution -
Let’s first look at the diagram,
 

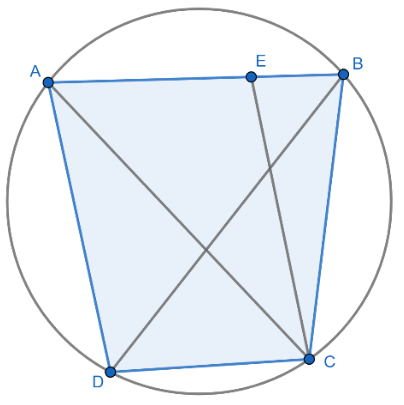
AC and BD are the diagonals and the line CE is parallel to AD.
We know that the opposite angles of a parallelogram are equal.
Therefore, $\angle D=\angle AEC..........(1)$
Now we also know that the sum of opposite angles of a cyclic quadrilateral is 180 degree.
Therefore, $\angle D+\angle ABC=180..........(2)$
From (1) and (2) we can say that,
$\angle AEC+\angle ABC=180........(3)$
Now angle AEC and CEB are linear pair,
Therefore, $\angle AEC+\angle CEB=180.........(4)$
Now again from (3) and (4) we can say that,
$\angle ABC=\angle CEB$
We know that the sides opposite the equal angles are also equal.
Therefore, from $\angle ABC=\angle CEB$ we get
CE = CB ………(5)
But we know that AECD is a parallelogram and hence opposite sides must be equal.
Therefore,
CE = AD ……….(6)
Therefore, from (5) and (6) we can say that
AD = CB ……….(7)
Thus the cyclic trapezium ABCD is isosceles.
Now for the second part,
We have the diagonals as AC and BD.
In triangle DBA and CBA,
AD = CB from (7)
AB = AB common side.
$\angle ADB=\angle ACB$( angles in the same segment of a circle are equal )
Hence, from the SAS rule.
Triangle ABD and ABC are congruent.

Note: All the properties of triangle and circle that we have used must be kept in mind. Cyclic quadrilateral is the quadrilateral which has the sum of opposite angles must be equal to 180.This is also a very important property of the cyclic quadrilateral which makes itself unique from the other quadrilaterals.