Question

Prove that: A line is drawn from one end point of a chord of a circle and if the angle between the chord and the line is half the measure of the arc intercepted by that angle then that line is a tangent to the circle.

Answer 1

Hint: We denote the chord as PQ, the line as $\overleftrightarrow{TR}$ which passes through Q. We are given from the question $\angle PQR=\dfrac{1}{2}m\left( \text{arc }PSQ \right),\angle PQT=\dfrac{1}{2}m\left( \text{arc }PUQ \right)$. We prove $\overleftrightarrow{TR}$ is tangent to the circle by proving $m\angle OQR={{90}^{\circ }}$ since radius perpendicular to tangent. We prove by taking the sum of angles of the isosceles triangle POQ.\[\]

Complete step-by-step solution
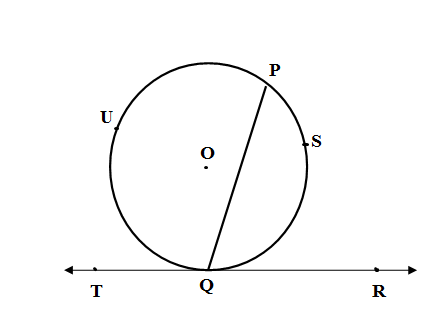
We are given that a line is drawn from one end point of a chord of a circle and the angle between the chord and the line is half the measure of the arc intercepted by that angle. Let the chord be PQ and let that line be $\overleftrightarrow{TR}$ such that $\overleftrightarrow{TR}$ passes through Q, one of the endpoints of the chord PQ. The angle between the chord and the line is $\angle PSQ$ and $\angle PQT$. Let PQ divide the circle into two arcs: arc PUQ and arc PSQ. We are given
\[\begin{align}
  & \angle PQR=\dfrac{1}{2}m\left( \text{arc }PSQ \right) \\
 & \angle PQT=\dfrac{1}{2}m\left( \text{arc }PUQ \right) \\
\end{align}\]
We have to prove TR is a tangent to the circle which means by tangent theorem we have to prove if O is the center $\angle OQR=\angle OQT={{90}^{\circ }}$ since the radius is always perpendicular to the tangent. \[\]

Let us join the PO and QO. \[\]

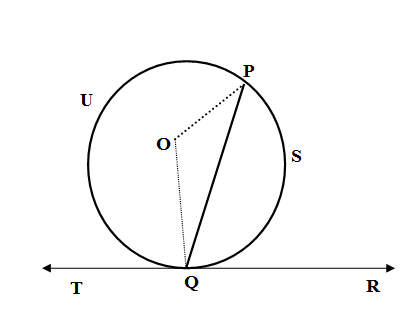
We know the measure of an arc is the measure of a smaller angle (called central angle) it subtends at the centre. So we have,
\[m\left( \text{arc }PSQ \right)=\text{Obtuse }m\angle POQ\]
So have from the given we have
\[\Rightarrow m\angle PQR=\dfrac{1}{2}m\angle POQ\]
We observe the triangle POQ which has equal sides as radii $OP=OQ$ and so their opposite angles will be equal
\[m\angle OQP=m\angle OPQ\]
We know that the sum of angles in a triangle is${{180}^{\circ }}$. So we have in triangle POQ,
\[ \begin{align}
  & m\angle POQ+m\angle OPQ+m\angle OQP={{180}^{\circ }} \\
 & \Rightarrow m\angle POQ+m\angle OQP+m\angle OQP={{180}^{\circ }} \\
 & \Rightarrow m\angle POQ={{180}^{\circ }}-2m\angle OQP \\
\end{align}\]
Let us divide both sides of the above equation by 2. We have,
\[\begin{align}
  & \Rightarrow \dfrac{1}{2}m\angle POQ={{90}^{\circ }}-m\angle OQP \\
 & \Rightarrow m\angle PQR={{90}^{\circ }}-m\angle OQP\left( \because m\angle PQR=\dfrac{1}{2}m\angle POQ \right) \\
 & \Rightarrow m\angle PQR+m\angle OQP={{90}^{\circ }} \\
 & \Rightarrow m\angle OQR={{90}^{\circ }} \\
\end{align}\]
Hence the statement is proved. \[\]

Note: We note that if PQ will be the diameter the proof is obvious since O will lie on PQ. We can alternatively proof using the reflex angle $\angle POQ$ and taking the arc PUQ. The statement of the proof is converse of a theorem of the angle between tangent and secant which states that “If an angle has its vertex on the circle, it’s one side touches the circle and the other intersects the circle in one more point, then the measure of the angle is half the measure of its intercepted arc.”