
How do you prove that a shape given is a kite?

Answer
456.3k+ views
Hint: Here, in this question we are supposed to figure out how to prove that a given shape is a kite. In order to prove a certain shape is any specific quadrilateral all we have to do is to check whether all the properties of that specific quadrilateral are satisfied for that shape or not. In this question, we will have to see if all the conditions or properties of the kite are satisfied for the shape or not. If they are satisfied then it is a kite, otherwise not.
Complete step-by-step answer:
In order to check whether the shape satisfies all the conditions or properties of kite, we must first know all the properties of kite.
A kite is a rhombus whose all four sides are congruent. The properties of kite are as follows:
i.The opposite angles between unequal sides are equal.
ii.The two pairs of congruent triangles of the kite have a common base.
iii.Diagonals of kite intersect each other at right angles i.e.,
The diagonals bisect each other perpendicularly.
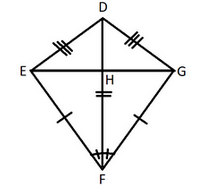
A diagram of a quadrilateral:
Here, we can see that,
The two pairs of adjacent sides are equal i.e., EF = GF, ED = GD
Diagonal DF is the angular bisector of angles
Diagonals intersect at right angles i.e., FD is perpendicular to EG
The shorter diagonal is bisected by the longer diagonal i.e., EH = HG
One pair of opposite angles is equal i.e.,
We can clearly see that these all are the properties of kite, since all the above five conditions are satisfied for a quadrilateral meaning it is a kite.
Note: The given question was a theoretical question. For figuring out whether a shape is a specific quadrilateral we must first know all the properties of that specific quadrilateral. A kite is a kind of rhombus. A rhombus is a four-sided quadrilateral whose all the sides are equal in length.
Complete step-by-step answer:
In order to check whether the shape satisfies all the conditions or properties of kite, we must first know all the properties of kite.
A kite is a rhombus whose all four sides are congruent. The properties of kite are as follows:
i.The opposite angles between unequal sides are equal.
ii.The two pairs of congruent triangles of the kite have a common base.
iii.Diagonals of kite intersect each other at right angles i.e.,
The diagonals bisect each other perpendicularly.
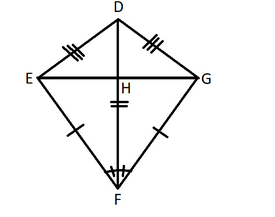
A diagram of a quadrilateral:

Here, we can see that,
The two pairs of adjacent sides are equal i.e., EF = GF, ED = GD
Diagonal DF is the angular bisector of angles
Diagonals intersect at right angles i.e., FD is perpendicular to EG
The shorter diagonal is bisected by the longer diagonal i.e., EH = HG
One pair of opposite angles is equal i.e.,
We can clearly see that these all are the properties of kite, since all the above five conditions are satisfied for a quadrilateral meaning it is a kite.
Note: The given question was a theoretical question. For figuring out whether a shape is a specific quadrilateral we must first know all the properties of that specific quadrilateral. A kite is a kind of rhombus. A rhombus is a four-sided quadrilateral whose all the sides are equal in length.
Recently Updated Pages
Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Questions & Answers - Ask your doubts

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Master Class 11 Science: Engaging Questions & Answers for Success

Trending doubts
What is the feminine gender of a stag class 8 english CBSE

How many ounces are in 500 mL class 8 maths CBSE

How many ten lakhs are in one crore-class-8-maths-CBSE

State the differences between manure and fertilize class 8 biology CBSE

What is the tagline of Swachh Bharat Abhiyaan A Sabka class 8 social studies CBSE

Find the cube root of 74088 class 8 maths CBSE




