Question

Prove that in any triangle, the side opposite to the larger angle is larger.

Answer 1

Hint:We know that the sides opposite to the equal sides are equal. Similarly the side opposite to the larger angle is larger.Using this concept we try prove the statement.


Complete step-by-step answer:
Generally this is the theorem that the side opposite to the larger angle is larger. So now let us see how.
Let $ABC$ be a triangle.

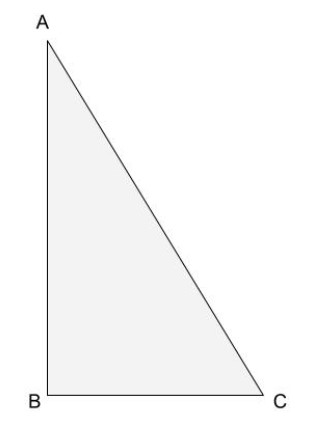
Let us assume that $\angle ABC > \angle ACB$
So if we prove that $AC > AB$, then it is clear that the side opposite to the larger angle is larger.
For this proof we need the construction.
So construct $BD$ on $AC$ such that $\angle DBC = \angle ACB$
As $\angle ABC > \angle ACB$, so we can find a point on $AC$ that is $D$ such that $\angle DBC = \angle ACB$.
As construction is done, it divides $\Delta ABC$ into two triangles that are $\Delta ABD$ and $\Delta DBC$.

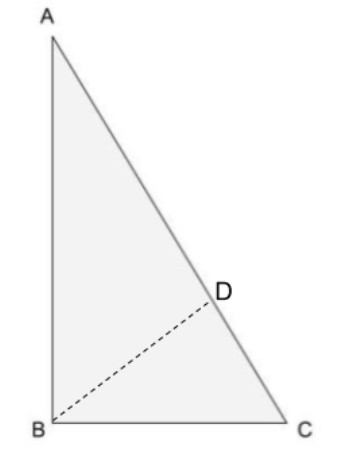
Now in $\Delta DBC$,
$\angle DBC = \angle ACB$
As we constructed $BD$ such that the two angles are equal.
Now we know that in the triangle, the sides opposite to equal angles are equal.
So $BD = DC$ $ - - - - - - - \left( 1 \right)$
Now we can add $AD$ on both sides of this above equation,
$AD + BD = DC + AD$
Now if solve $AD + DC$, we get $AC$
So $AD + BD = AC$
Or we can say that,
$AC = BD + AD$ $ - - - - - - - \left( 2 \right)$
Now in $\Delta ADB$,
We know that for any triangle to form, the sum of two sides will always be greater than the third side.
So $BD + AD > AB$ $ - - - - - - - - \left( 3 \right)$
Now putting the value of $AD + BD = AC$ in equation (3),
So we get $AC > AB$.
Hence it is proved that $AC > AB$ if $\angle ABC > \angle ACB$
Hence we can say that the side opposite to the larger angle is larger.

Note:Let for any triangle $ABC$, by applying the $\sin $ rule we get,
 

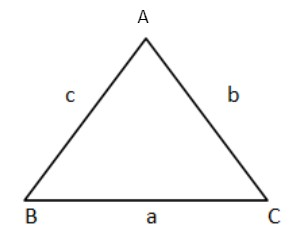
$\dfrac{{\sin A}}{a} = \dfrac{{\sin B}}{b} = \dfrac{{\sin C}}{c}$
So if $\angle A > \angle B$,
$\sin A > \sin B$ as $\sin $ is the increasing function.
So $\dfrac{{\sin A}}{a} = \dfrac{{\sin B}}{b}$
$a = \dfrac{{\sin A}}{{\sin B}}b$ and $\sin A > \sin B$
So $a > b$
Hence Proved.