Question

How do you prove that quadrilateral \[ABCD\] is a parallelogram \[A(-2,-1),B(1,2),C(5,2)\And D(2,-1)\] using slope?

Answer 1

Hint: A parallelogram is a quadrilateral in which the opposite sides are parallel and of equal length. To check whether a quadrilateral is a parallelogram or not. We have to check if its opposite sides are parallel. As we know that parallel sides have equal slopes, in other words, we have to check if the opposite sides have an equal slope or not. For any given two points, \[M(a,b)\And N(c,d)\] the slope of the line joining two points is \[\dfrac{d-b}{c-a}\].

Complete step-by-step answer:

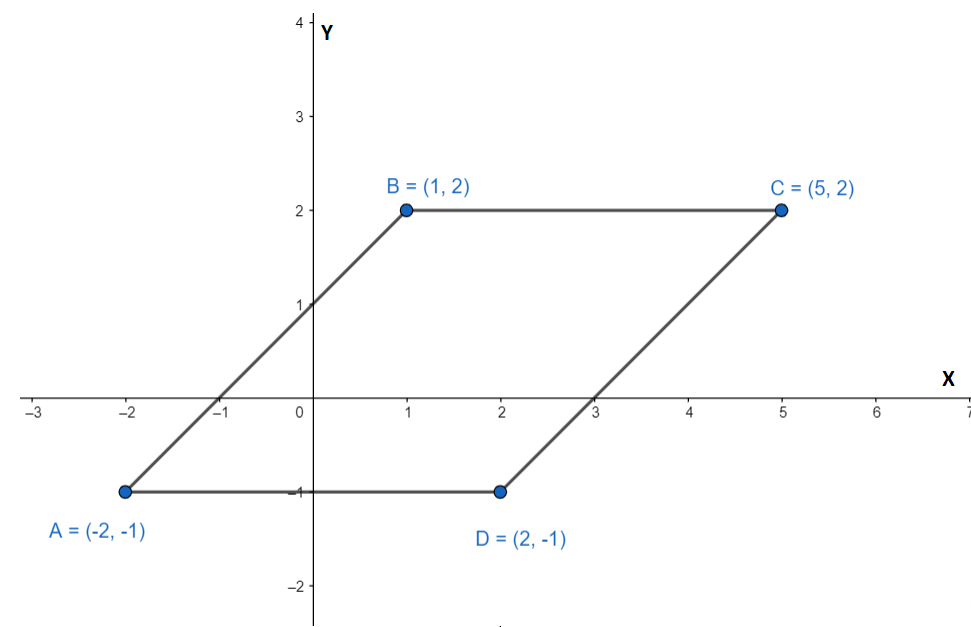
We are given the points \[A(-2,-1),B(1,2),C(5,2)\And D(2,-1)\]. We have to prove that these points make a parallelogram. As we know that the opposite sides of a parallelogram are parallel, which means that their slope is the same. We can prove that this is a parallelogram by showing that the slope of the opposite sides is the same. We know that, for any given two points, \[M(a,b)\And N(c,d)\] the slope of the line joining two points is \[\dfrac{d-b}{c-a}\]. We can find the slope of the line joining these points as follows,
For line joining \[A(-2,-1)\And B(1,2)\], the slope of the line \[AB\]\[=\dfrac{2-(-1)}{1-(-2)}=\dfrac{2+1}{1+2}=\dfrac{3}{3}=1\]
For the line joining \[B(1,2)\And C(5,2)\], the slope of the line \[BC=\dfrac{2-2}{5-1}=0\].
For the line joining \[C(5,2)\And D(2,-1)\], the slope of the line \[CD=\dfrac{-1-2}{2-5}=\dfrac{-3}{-3}=1\].
For the line joining the \[A(-2,-1)\And D(2,-1)\], the slope of the line \[AD=\dfrac{-1-(-1)}{2-(-2)}=0\].
From the above values, we can say that \[AB\And CD\] and \[BC\And DA\] are parallel as their slopes are equal.
Hence the quadrilateral \[ABCD\] is a parallelogram.
We can also plot the points on the graph as follows,

Note: One should remember the properties of the sides, angles, diagonals of different types of quadrilaterals to solve these types of questions. Here if we calculate the length of the sides \[AB,BC,CD,\And AD\] they are \[3\sqrt{2},4,3\sqrt{2}\And 4\] respectively. Hence the opposite side length is the same, we can use this also to prove that the quadrilateral that is formed with these points is a parallelogram.