Question

Prove that the all circles described on focal radii as radius with centre as the endpoint of the focal radius which is on the parabola touch the directrix of the parabola. Prove that all the circles described on focal as diameters touch the tangent at the vertex.

Answer 1

Hint: Use the fact that a general point on parabola ${{y}^{2}}=4ax$ is $P\left( a{{t}^{2}},2at \right)$ where t is a parameter. Use the fact that the equation of circle with diametric points as $\left( {{x}_{1}},{{y}_{1}} \right)$ and $\left( {{x}_{2}},{{y}_{2}} \right)$ is given by
${{x}^{2}}+{{y}^{2}}-\left( {{x}_{1}}+{{x}_{2}} \right)x-\left( {{y}_{1}}+{{y}_{2}} \right)y+{{x}_{1}}{{x}_{2}}+{{y}_{1}}{{y}_{2}}$=0. Hence determine the equation of the circle with diameter endpoints as the endpoints of a focal radius. Use the fact that if a line is tangent to a circle then the perpendicular distance of the line from the centre of the circle is equal to radius of the circle. Hence prove that the tangent at vertex is tangent to the circle. Similarly prove for the other case.

Complete step by step answer:
Part 1: When the circle is drawn taking the endpoints of the focal radius as diameter.

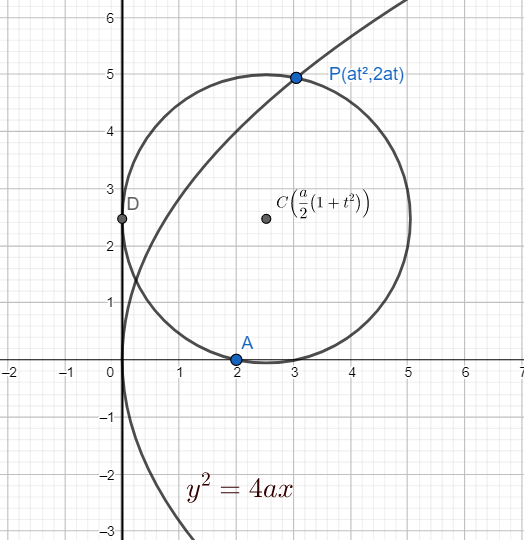
We know that the y-axis is tangent to the parabola at vertex.
Hence, we have
x = 0 is the equation of tangent to the parabola at vertex.
Let the point P on the parabola have coordinates $P\left( a{{t}^{2}},2at \right)$.
We know that the coordinates of focus are $\left( a,0 \right)$.
Hence the coordinates of the centre of the circle is $C\left( \dfrac{a{{t}^{2}}+a}{2},at \right)=\left( \dfrac{a}{2}\left( {{t}^{2}}+1 \right),at \right)$
Also, let r be the length of the radius of the circle.
Hence, we have
$\begin{align}
  & PA=2r \\
 & \Rightarrow 2r=\sqrt{{{\left( a{{t}^{2}}-a \right)}^{2}}+4{{a}^{2}}{{t}^{2}}}=a\sqrt{{{\left( {{t}^{2}}-1 \right)}^{2}}+4{{t}^{2}}} \\
\end{align}$
We know that ${{\left( a-b \right)}^{2}}+4ab={{\left( a+b \right)}^{2}}$
Hence, we have
$2r=a\left( {{t}^{2}}+1 \right)$
Hence, we have
$r=\dfrac{a}{2}\left( 1+{{t}^{2}} \right)$
We know that the distance of point P(x,y) y-axis is x.
Hence, the distance of centre of the circle from y-axis is $\dfrac{a}{2}\left( 1+{{t}^{2}} \right)$ which is equal to radius of the circle and hence y-axis is tangent to the circle.
Hence the tangent to the parabola at vertex is tangent to the circle.
Part 2: When the circle is drawn with centre as a point on the parabola and radius equal to focal radius of the parabola at that point.

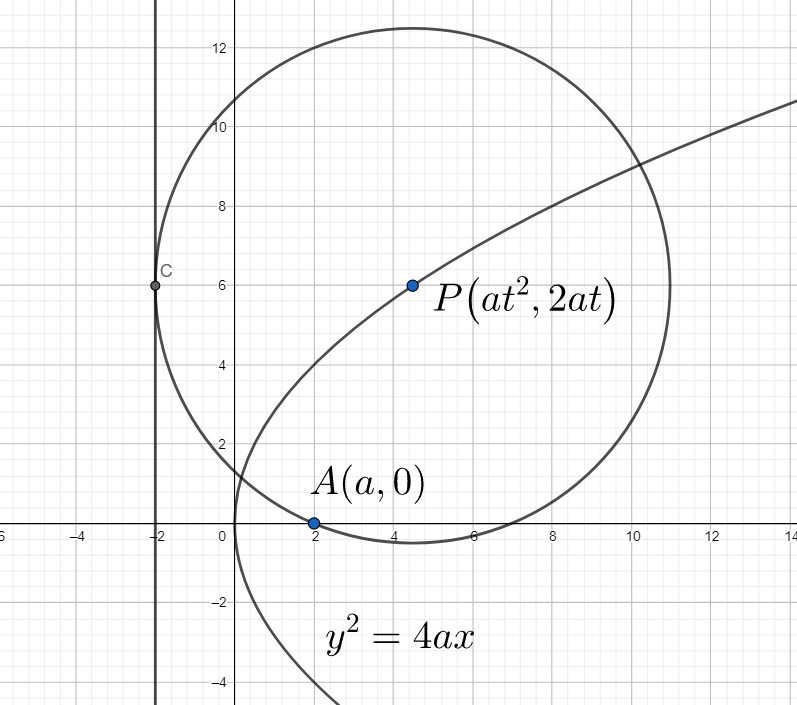
Here the radius of the circle is equal to PA.
We calculated PA above.
Hence, we have
$r=a\left( {{t}^{2}}+1 \right)$
Also, equation of directrix is $x=-a$
Hence the distance of point P from the directrix is $a{{t}^{2}}+a=a\left( {{t}^{2}}+1 \right)$
Hence x = -a is tangent to the circle.
Hence proved.

Note: [1] We can also solve the question by showing that the line intersects the circle at only on point by showing that the discriminant of the resulting quadratic equation in x formed by eliminating y from the two equations (the equation of the circle and the equation of the line) is 0. This method is however tedious and prone to calculation mistakes and should be avoided.