Question

Prove that the area of the equilateral triangle described on the side of a square is half the area of the equilateral triangle described on its diagonal.

Answer 1

Hint- In order to prove such questions we will use the property of two similar triangles as the ratio of two similar triangles is equal to the square of the ratio of their corresponding sides and we also know the diagonal of the square is $\sqrt 2 $ time of its sides. Use these properties to reach the answer.

Complete step-by-step answer:

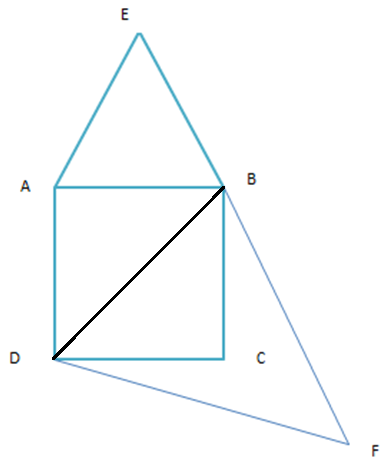
Let ABCD is a square, AEB is an equilateral triangle described on the side of the square
And DBF is an equilateral triangle described on a diagonal BD of the square.

We have to prove that\[\dfrac{{Area\left( {\Delta DBF} \right)}}{{Area\left( {\Delta AEB} \right)}}{\text{ }} = {\text{ }}\dfrac{2}{1}\]

Proof-
 If two equilateral triangles are similar then all angles are = 60 degrees.

Therefore, by AAA similarity criterion,\[\Delta DBF{\text{ }}\sim\Delta AEB\]

\[\dfrac{{Ar\left( {\Delta DBF} \right)}}{{Ar\left( {\Delta AEB} \right)}}{\text{ }} = {\text{ }}\dfrac{{D{B^2}}}{{A{B^2}}}\;...............(1)\]

We know that the ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding sides.

But, we have \[DB = \sqrt 2 AB\] ……….. (2) [ Diagonal of square is $\sqrt 2 $ times of its side]

Substitute equation (2) in equation (1), we get

\[
  \dfrac{{Ar\left( {\Delta DBF} \right){\text{ }}}}{{Ar\left( {\Delta AEB} \right)}} = \dfrac{{\dfrac{{\sqrt 3 }}{4}{{\left( {\sqrt 2 AB{\text{ }}} \right)}^2}\;}}{{\dfrac{{\sqrt 3 }}{4}A{B^2}}}{\text{ }}\left[ {\because {\text{area of equilateral triangle of side a}} = \dfrac{{\sqrt 3 }}{4}{a^2}} \right] \\
  \dfrac{{Ar\left( {\Delta DBF} \right){\text{ }}}}{{Ar\left( {\Delta AEB} \right)}} = \dfrac{{{{\left( {\sqrt 2 AB{\text{ }}} \right)}^2}\;}}{{A{B^2}}} \\
  \; = \;\dfrac{{2A{B^2}}}{{A{B^2}\;}} = \dfrac{2}{1} \\
 \]
So, the area of the equilateral triangle described on one side of the square is equal to half the area of the equilateral triangle described on one of its diagonals.

Note- In order to solve these types of problems related to the property of triangles first of all remembers all the properties and theorems of the triangle. Secondly, see the conditions given in the question and with the help of given condition and theorem solve the questions in steps. Such as in the above problem we use the equal area criterion and a theorem.