
Prove that the chords equidistant from the center of a circle are equal in length.
Answer
519.6k+ views
Hint: First of all, draw a circle with center O and chords AB and CD at a distance of OX and OY from the center respectively. Now, join O to A and O to D. Now prove
Complete step-by-step answer:
In this question, we have to prove that the chords equidistant from the center of a circle are equal in length. First of all, construct a circle with center O
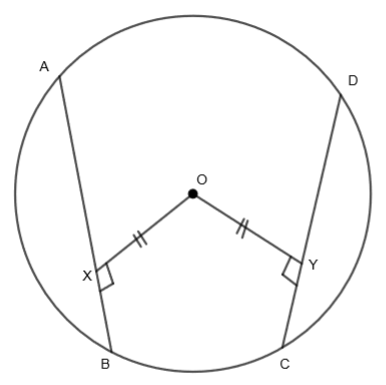
In the above circle, AB and CD are two chords of the circle where OX is the distance from the center of the chord AB that is
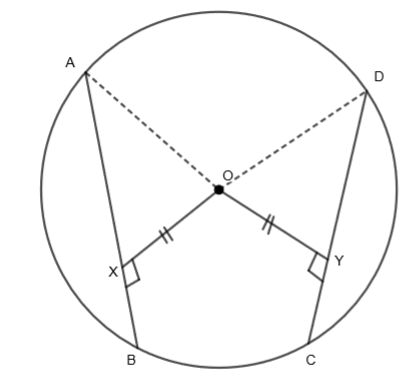
Consider
We know that in a circle, all radii are equal. So,
OA = OD …..(ii)
Also, we are given that OX = OY……(iii)
So, from right angle hypotenuse side (RHS) congruence criteria, we get,
We know that the corresponding parts of the congruent triangles are equal. So, we get,
AX = DY……(iv)
We know that the perpendicular from the center to a chord bisects the chord. So, we get,
For chord AB, X bisects AB, so AB = 2 AX.
For chord CD, Y bisects CD, so, CD = 2 DY
Now by substituting the values of AX and DY from equation (v) and (vi) in equation (iv), we get,
AB = CD [Hence proved]
So, we have proved that chords equidistant from the center of the circle is equal in length.
Note: In this question, students must remember all the theorems discussed in the above solution as they are very useful while solving the questions related to the circle. Also, students can check these theorems practically by constructing a circle of a certain radius and making equidistant chords and perpendiculars on it from the center. Now, measure the lengths of both the chords if they are equal or not.
Complete step-by-step answer:
In this question, we have to prove that the chords equidistant from the center of a circle are equal in length. First of all, construct a circle with center O

In the above circle, AB and CD are two chords of the circle where OX is the distance from the center of the chord AB that is

Consider
We know that in a circle, all radii are equal. So,
OA = OD …..(ii)
Also, we are given that OX = OY……(iii)
So, from right angle hypotenuse side (RHS) congruence criteria, we get,
We know that the corresponding parts of the congruent triangles are equal. So, we get,
AX = DY……(iv)
We know that the perpendicular from the center to a chord bisects the chord. So, we get,
For chord AB, X bisects AB, so AB = 2 AX.
For chord CD, Y bisects CD, so, CD = 2 DY
Now by substituting the values of AX and DY from equation (v) and (vi) in equation (iv), we get,
AB = CD [Hence proved]
So, we have proved that chords equidistant from the center of the circle is equal in length.
Note: In this question, students must remember all the theorems discussed in the above solution as they are very useful while solving the questions related to the circle. Also, students can check these theorems practically by constructing a circle of a certain radius and making equidistant chords and perpendiculars on it from the center. Now, measure the lengths of both the chords if they are equal or not.
Latest Vedantu courses for you
Grade 10 | MAHARASHTRABOARD | SCHOOL | English
Vedantu 10 Maharashtra Pro Lite (2025-26)
School Full course for MAHARASHTRABOARD students
₹33,300 per year
Recently Updated Pages
Master Class 10 General Knowledge: Engaging Questions & Answers for Success

Master Class 10 Computer Science: Engaging Questions & Answers for Success

Master Class 10 Science: Engaging Questions & Answers for Success

Master Class 10 Social Science: Engaging Questions & Answers for Success

Master Class 10 Maths: Engaging Questions & Answers for Success

Master Class 10 English: Engaging Questions & Answers for Success

Trending doubts
A boat goes 24 km upstream and 28 km downstream in class 10 maths CBSE

Why is there a time difference of about 5 hours between class 10 social science CBSE

The British separated Burma Myanmar from India in 1935 class 10 social science CBSE

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

Chandigarh is the capital of A Punjab B Haryana C Punjab class 10 social science CBSE

What are the public facilities provided by the government? Also explain each facility




