Question

Prove that the diagonals of a rhombus bisect each other at right angles.

Answer 1

Hint: In this case, we have to prove that the diagonals of a rhombus bisect each other and they do so at right angles. Therefore, first we should show that the triangles made at opposite sides by the diagonals and sides are congruent and use it to show that the diagonals bisect each other. Then, we shall again use the property of congruence to prove that the angle between the diagonals is ${{90}^{\circ }}$.

Complete step-by-step answer:

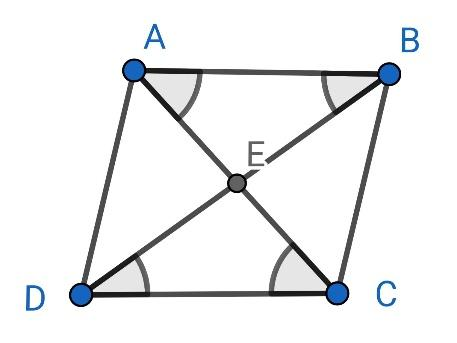
Let ABCD represent the rhombus. We need to show that the diagonals bisect each other, i.e.
AE=EC and DE=EB

Two triangles are said to be congruent by the AAS criterion if the values of two angles and the length of one side is the same in both the triangles………… (1.1)

Also, as we know that a rhombus is also a parallelogram, \[AB||DC\] and \[DA||CB\]. Therefore, as the corresponding angles made by two parallel lines and a transversal are equal,

\[\angle EDC=\text{ }\angle EBA\ldots \ldots (1.2)\]

\[\angle ECD=\angle EAB\ldots \ldots .(1.3)\]

Also, in a rhombus, opposite sides are equal, therefore,

\[DC=AB..................(1.4)\]

Therefore, by the AAS congruence condition stated in equation (1.1), and using equations (1.2), (1.3) and (1.4), \[\Delta DEF\] is congruent to \[\Delta BEA\].


Now, the sides enclosing the same angles in two congruent triangles have the same length. Therefore,

\[AE=EC\text{ }and\text{ }DE=EB.................(1.5)\]

Thus, the diagonals bisect each other.


Now, we have to prove that the diagonals bisect each other at right angles, i.e.,

\[\angle AED=\angle DEC={{90}^{\circ }}\]

For it, we shall use another criterion of congruence as

Two triangles are said to be congruent by the SSS criterion if the lengths of all the sides are the same in both the triangles………… (1.6)

Now, as all the sides are equal in a rhombus, we have,

\[AD=DC....................(1.7)\]

Also,

\[DE=DE\text{ }\left( common\text{ }side \right)...............(1.8)\]

\[AE=EC\text{ }\left( \text{ }from\text{ }(1.5) \right)...............(1.9)\]

Therefore, by SSS congruence criterion,

\[\Delta AED\text{ }is\text{ }congruent\text{ }to\text{ }\Delta CED\text{ i}\text{.e}\text{. }\Delta AED\cong \Delta CED...........(1.10)\]


As the angles enclosing the corresponding sides of congruent triangles have the same value,
\[\angle AED=\text{ }\angle CED...............(1.11)\]

However, as AC is a straight line, we should have

\[\begin{align}

  & \angle AED+\angle CED={{180}^{\circ }}\Rightarrow \angle AED+\angle AED={{180}^{\circ }}(from(1.11)) \\

 & \Rightarrow \angle AED=\dfrac{{{180}^{\circ }}}{2}={{90}^{\circ }}.................(1.12) \\

\end{align}\]

Also, from equations (1.10) and (1.11),

\[\angle CED=\angle AED={{90}^{\circ }}....................(1.13)\]

Thus from equations (1.5) and (1.13), we have proved that the diagonals of a rhombus bisect each other at right angles.


Note: We should be careful to write the notation of triangles in a correct way to express the congruence condition. For, example, in equation (1.10), \[\Delta AED\cong \Delta CED\]cannot be written as \[\Delta AED\cong \Delta ECD\]because the ordering of the vertices of the triangle is not correct in the second case (\[\Delta CED\] has been written as \[\Delta ECD\]) .