
Prove that the equal chords of two congruent circles subtend equal angles at their respective centres.
Answer
431.4k+ views
2 likes
Hint: Use the fact that the radii of two congruent circles are equal and hence prove that OA = O’A’ and OB = O’B’. Use the fact that since the chords are equal AB = A’B’ and hence prove that the triangle ABC and A’B’C’ are congruent and hence prove that
Complete step by step answer:
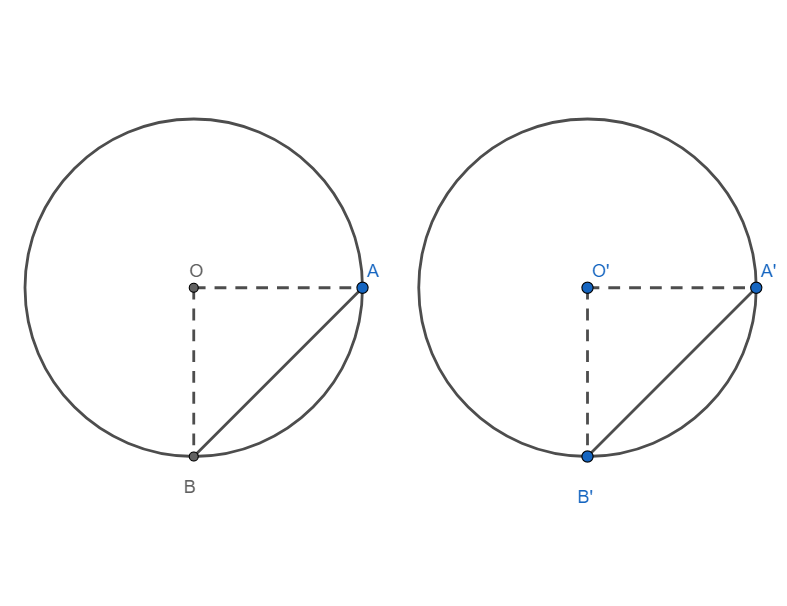
Given: Two circles with centre O and O’ have equal radii. AB is the chord of the circle with centre O and A’B’ is a chord of the circle with centre O’.
To prove
Proof:
Since the circle have equal radii, we have
OA = O’A’ and OB = O’B’
Now, in triangle AOB and A’O’B’, we have
AO = A’O’ (proved above)
OB = O’B’ (Proved above)
AB = A’B’ (Given).
Hence by S.S.S congruence criterion, we have
Hence, we have
Hence, equal chords of two congruent circles subtend equal angles at their respective centres.
Hence, proved.
Note: Alternative Solution: Using Sine rule.
We know that if R is the radius of circumcentre of a triangle ABC, then
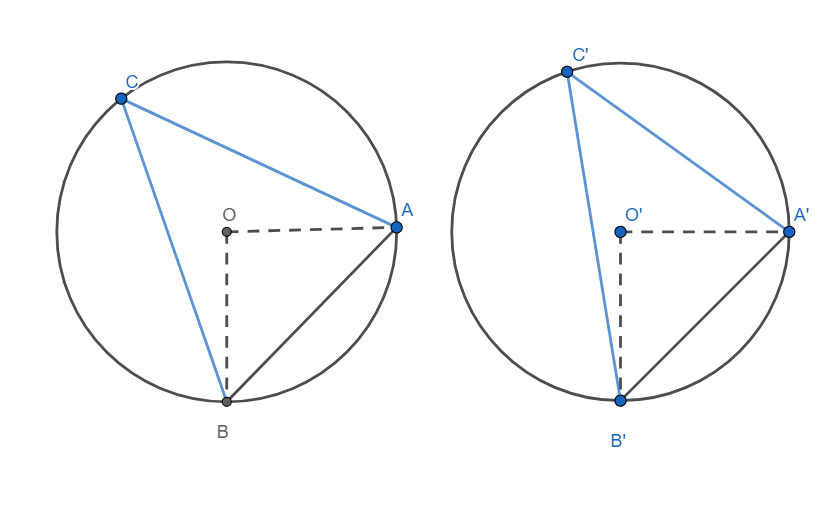
Consider two points C and C’ on the alternate segments as shown in the diagram above.
By sine rule, we have
Similarly, we have
Since AB = A’B’, we have
We know that the angle subtended in the alternate segment is half the angle subtended at the centre.
Hence, we have
Since
Q.E.D
Complete step by step answer:

Given: Two circles with centre O and O’ have equal radii. AB is the chord of the circle with centre O and A’B’ is a chord of the circle with centre O’.
To prove
Proof:
Since the circle have equal radii, we have
OA = O’A’ and OB = O’B’
Now, in triangle AOB and A’O’B’, we have
AO = A’O’ (proved above)
OB = O’B’ (Proved above)
AB = A’B’ (Given).
Hence by S.S.S congruence criterion, we have
Hence, we have
Hence, equal chords of two congruent circles subtend equal angles at their respective centres.
Hence, proved.
Note: Alternative Solution: Using Sine rule.
We know that if R is the radius of circumcentre of a triangle ABC, then

Consider two points C and C’ on the alternate segments as shown in the diagram above.
By sine rule, we have
Similarly, we have
Since AB = A’B’, we have
We know that the angle subtended in the alternate segment is half the angle subtended at the centre.
Hence, we have
Since
Q.E.D
Recently Updated Pages
Master Class 9 General Knowledge: Engaging Questions & Answers for Success

Master Class 9 English: Engaging Questions & Answers for Success

Master Class 9 Science: Engaging Questions & Answers for Success

Master Class 9 Social Science: Engaging Questions & Answers for Success

Master Class 9 Maths: Engaging Questions & Answers for Success

Class 9 Question and Answer - Your Ultimate Solutions Guide

Trending doubts
State and prove Bernoullis theorem class 11 physics CBSE

What are Quantum numbers Explain the quantum number class 11 chemistry CBSE

Who built the Grand Trunk Road AChandragupta Maurya class 11 social science CBSE

1 ton equals to A 100 kg B 1000 kg C 10 kg D 10000 class 11 physics CBSE

State the laws of reflection of light

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE




