
Prove that the intercept of a tangent between two parallel tangents to a circle subtends a right angle at the center.
Answer
528.3k+ views
Hint: Line joining the parallel tangents will be straight line and will pass through the centre as well. Choose the triangles consisting of angles subtending at centre by the intercept of tangent and prove them congruent to each other. Draw a neat diagram to observe those triangles. Use the RHS property to prove the angles to be congruent. Angle by a straight line is
Complete step-by-step solution -
Here, it is given that the tangents drawn are parallel and hence, we need to prove that the intercept of the tangent between two parallel tangents to a circle subtends at a right angle at centre.
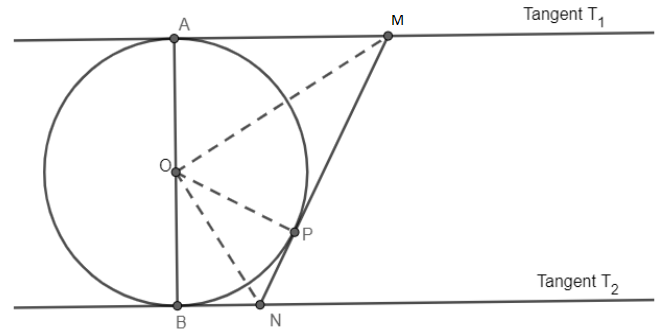
where OA, OB and OP are the radius of the circle and AM, BM, MN are parts of the tangents.
Now, it is given that the tangents
It means line AB will be a straight line and angle AOB will be
So, we get
Now, we know the angle made at the touching point of the tangent to the circle, with the tangent and radius is
Now, in
OM=OM (common)
OA = OP = Radius (Radius of circle)
Hence,
Similarly, we can prove angle NOP and angle BON as equal angles using the same approach.
As,
ON = ON (common)
OP=OB (radius)
Hence,
Now, we can observe the angle AOB which can be written as sum of angles
Now, put
Now, we can replace
Now, we can replace
So, the angle subtended by the tangent MN is
Hence, the given statement is proved
Note: One may confuse with the statement that the line AOB will be straight and from angle as
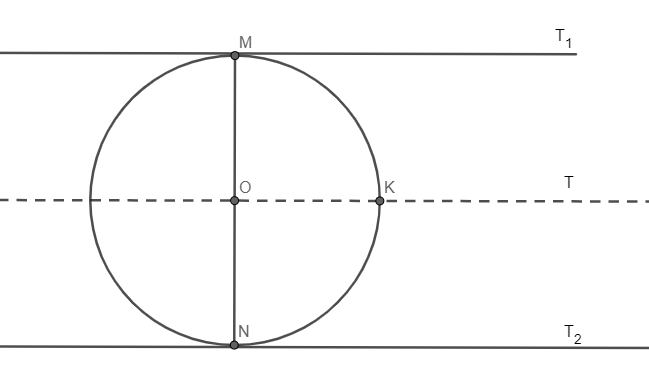
Proof:
Given:
Construction: Draw a line passing through centre O, and parallel to both the tangents
Proof:
As we know, angles made by transversal on the same side of two parallel lines has sum of
Similarly,
So,
RHS criteria means one angle of both the triangles should be
Complete step-by-step solution -
Here, it is given that the tangents drawn are parallel and hence, we need to prove that the intercept of the tangent between two parallel tangents to a circle subtends at a right angle at centre.

where OA, OB and OP are the radius of the circle and AM, BM, MN are parts of the tangents.
Now, it is given that the tangents
It means line AB will be a straight line and angle AOB will be
So, we get
Now, we know the angle made at the touching point of the tangent to the circle, with the tangent and radius is
Now, in
OM=OM (common)
OA = OP = Radius (Radius of circle)
Hence,
Similarly, we can prove angle NOP and angle BON as equal angles using the same approach.
As,
ON = ON (common)
OP=OB (radius)
Hence,
Now, we can observe the angle AOB which can be written as sum of angles
Now, put
Now, we can replace
Now, we can replace
So, the angle subtended by the tangent MN is
Hence, the given statement is proved
Note: One may confuse with the statement that the line AOB will be straight and from angle as

Proof:
Given:
Construction: Draw a line passing through centre O, and parallel to both the tangents
Proof:
As we know, angles made by transversal on the same side of two parallel lines has sum of
Similarly,
So,
RHS criteria means one angle of both the triangles should be
Recently Updated Pages
Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Questions & Answers - Ask your doubts

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Master Class 11 Science: Engaging Questions & Answers for Success

Trending doubts
A boat goes 24 km upstream and 28 km downstream in class 10 maths CBSE

Why is there a time difference of about 5 hours between class 10 social science CBSE

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

What is the full form of POSCO class 10 social science CBSE

Change the following sentences into negative and interrogative class 10 english CBSE

How do you prove that the diagonals of a rectangle class 10 maths CBSE




