
Prove that the perpendicular bisector of a chord of a circle passes through the center.
Answer
521.4k+ views
4 likes
Hint: We will assume that C is not the centre of the circle and try to prove that
Complete step-by-step answer:
It is given in the question that the perpendicular bisector of a chord of a circle always passes through the centre of the circle. Let us assume that ‘S’ is a circle in which AB is chord, CD is perpendicular bisector of chord AB at D as shown,
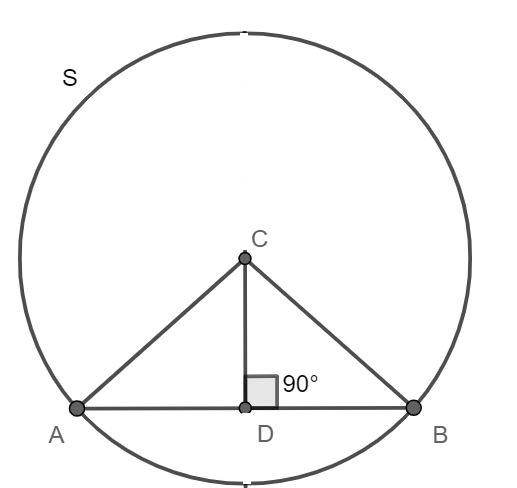
We will first assume that C is not the centre of the circle. Now, in
From the above three conditions or equations, we can say that
We know that in congruent triangles sides and angles have equal measurements, thus we can say that side AC of triangle ADC is equal to side BC of triangle BDC, that is
But if we conclude that side AC is equal to side BC then this contradicts our assumption that C is not the centre of the circle. We are saying this because the centre of the circle is the only point within the circle that has the point on the circumference equal distance from it.
Here, point C has two points A and B having equal distance, thus from this, we can say that ‘C’ is the centre of the circle. Thus, it is proved that the perpendicular bisector of the chord passes through the centre of the circle.
Hence Proved.
Note: Students may get confused with the word chord and arc, they may assume that both are the same thing but it is not actually true. Even in this question students may assume that arc AB is perpendicularly bisected by CD but in question it is very clearly given that AB is a chord and CD is bisector. Thus, it is recommended to know the actual meaning of the terms by referring to the definition of terms.
Complete step-by-step answer:
It is given in the question that the perpendicular bisector of a chord of a circle always passes through the centre of the circle. Let us assume that ‘S’ is a circle in which AB is chord, CD is perpendicular bisector of chord AB at D as shown,

We will first assume that C is not the centre of the circle. Now, in
From the above three conditions or equations, we can say that
We know that in congruent triangles sides and angles have equal measurements, thus we can say that side AC of triangle ADC is equal to side BC of triangle BDC, that is
But if we conclude that side AC is equal to side BC then this contradicts our assumption that C is not the centre of the circle. We are saying this because the centre of the circle is the only point within the circle that has the point on the circumference equal distance from it.
Here, point C has two points A and B having equal distance, thus from this, we can say that ‘C’ is the centre of the circle. Thus, it is proved that the perpendicular bisector of the chord passes through the centre of the circle.
Hence Proved.
Note: Students may get confused with the word chord and arc, they may assume that both are the same thing but it is not actually true. Even in this question students may assume that arc AB is perpendicularly bisected by CD but in question it is very clearly given that AB is a chord and CD is bisector. Thus, it is recommended to know the actual meaning of the terms by referring to the definition of terms.
Recently Updated Pages
Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Questions & Answers - Ask your doubts

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Master Class 11 Science: Engaging Questions & Answers for Success

Trending doubts
A boat goes 24 km upstream and 28 km downstream in class 10 maths CBSE

Why is there a time difference of about 5 hours between class 10 social science CBSE

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

What is the full form of POSCO class 10 social science CBSE

Change the following sentences into negative and interrogative class 10 english CBSE

How do you prove that the diagonals of a rectangle class 10 maths CBSE




