Question

Prove that the sum of 4 angles in a quadrilateral is $360$?

Answer 1

Hint: Here in this question, we have to prove that the sum of the angles of a quadrilateral is equal to ${360^ \circ }$. For this, first we need to consider any one of the quadrilateral and partition or divide it into the two triangles then we know that the sum of interior angles of a triangle is ${180^ \circ }$ then their sum gives the required solution.

Complete step by step answer:
A quadrilateral is a polygon, which is a flat closed two-dimensional shape with four edges and four vertices. The other names for quadrilateral include quadrangle and tetragon.There are 5 types of quadrilaterals: Square, Rectangle, Parallelogram, Trapezium or Trapezoid, kite, and Rhombus.

Consider the given question:we need to prove that the sum of 4 angles in a quadrilateral is $360$. Let us consider rectangle $ABCD$ which is one of the type of quadrilateral:

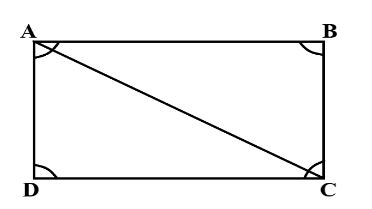
In rectangle or quadrilateral $ABCD$ draw a diagonal $AC$ which divides the rectangle into two triangles $\vartriangle \,ABC$ and $\vartriangle \,ADC$.
$ \Rightarrow \,\,$Sum of angles of quadrilateral $ABCD$ $= $ sum of angles of $\vartriangle \,ABC$ $ + $ sum of the angles $\vartriangle \,ADC$.
we know that sum of the angles of a triangle is ${180^ \circ }$, then
$ \Rightarrow \,\,$Sum of angles of quadrilateral $ABCD$ $= $ ${180^ \circ }$ + ${180^ \circ }$
$\therefore \,\,\,$Sum of angles of quadrilateral $ABCD$ $= $ ${360^ \circ }$.
$\therefore \,\,\,\,\angle ABC + \angle BCD + \angle CDA + \angle DAC = {360^ \circ }$.
Hence proved.

Note: Remember, a triangle's angles add up to ${180^ \circ }$ because one exterior angle is equal to the sum of the other two angles in the triangle. In other words, the other two angles in the triangle (the ones that add up to form the exterior angle) must combine with the third angle to make a ${180^ \circ }$ angle.