Question

Prove that the tangents drawn from an external point to a circle are of equal lengths.

Answer 1

Hint: Assume a circle with center O and radius r. Then from as external point P draw two tangents PQ and PR to the circle. We know that the radius is perpendicular to the point on the circle where the tangent touches the circle. It means that \[\angle OQP=\angle ORP={{90}^{0}}\]. Then prove that the \[\Delta OQP\] is congruent to the \[\Delta ORP\]. If two triangles are congruent then we can say that the sides of one triangle are equal to the sides of another triangle.

Complete step-by-step solution -

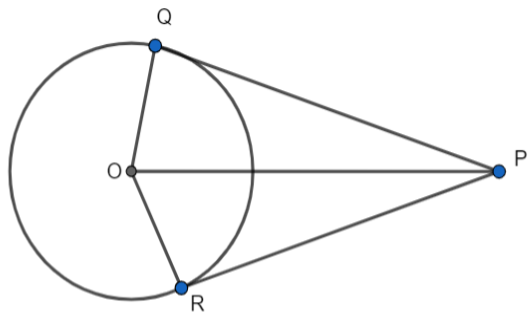
Let us assume a circle with center O and radius r. Here P is an external point. From point P we have drawn two tangents that are PQ and PR to the circle.
We know that the radius is perpendicular to the point on the circle where the tangent touches the circle. It means that \[\angle OQP=\angle ORP={{90}^{0}}\] .
In \[\Delta OQP\] and \[\Delta ORP\] , we have
\[\angle OQP=\angle ORP={{90}^{0}}\]
\[OP=OP\] (common in both triangles)
\[OQ=OR\] (radius of the circle)
\[\Delta OQP\cong \Delta ORP\] (Right Hypotenuse Side)
Thus, \[\Delta OQP\] and \[\Delta ORP\] are congruent with each other.
It means sides of \[\Delta OQP\] and \[\Delta ORP\] are equal to each other.
So, \[PQ=PR\] .
Here, PQ and PR are the tangents drawn from an external point and both are equal.
Hence, tangents drawn from an external point to a circle are of equal length.

Note: This question can also be solved by using a property that the line joining the center of a circle and an external point from which the tangents are drawn is the angle bisector.

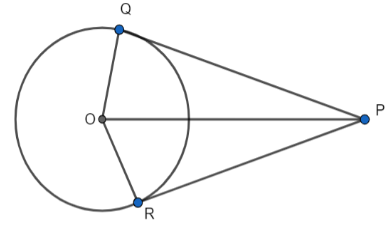
It means that OP is the angle bisector of the \[\angle QPR\] .
We can say that, \[\angle QPO=\angle OPR\] .
\[\angle QOP={{90}^{0}}-\angle QPO\]
\[\angle ROP={{90}^{0}}-\angle OPR\]
We can say that, \[\angle QOP=\angle ROP\] .
In \[\Delta OQP\] and \[\Delta ORP\] , we have
\[OQ=OR\] (radius of the circle)
\[\angle QOP=\angle ROP\]
\[OQ=OR\] (radius of the circle)
\[\Delta OQP\cong \Delta ORP\] (Side Angle Side)
Thus, \[\Delta OQP\] and \[\Delta ORP\] are congruent with each other.
So, \[PQ=PR\] .
Hence, tangents drawn from an external point to a circle are of equal length.