Question

Prove that two triangles having the same base (or equal bases) have equal areas between the same parallels.

Answer 1

Hint: Assume two triangles between two parallel lines having the same base. We know the formula of the area of the triangle, \[Area=\dfrac{1}{2}\times Base\times Height\] . We also know the property that the distance between parallel lines is always constant. So, each perpendicular distance between the parallel lines is always equal to each other. Now, solve it further.

Complete step-by-step answer:

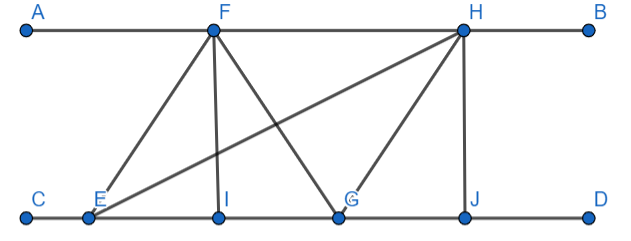
Assume two line segments AB and CD parallel to each other and two triangles which are \[\Delta FEG\] and \[\Delta HEG\] having the same base EG.
Let the distance between the parallel lines AB and CD be x.
In \[\Delta FEG\] , we have,
EG as the base of the \[\Delta FEG\] ,
FI is the height which is also perpendicular to the base EG.
We know the formula of the area of the triangle,
\[Area=\dfrac{1}{2}\times Base\times Height\]
Now, using this formula to get the area of the \[\Delta FEG\] .
Area of \[\Delta FEG\] = \[\dfrac{1}{2}\times EG\times FI\] ………………………..(1)
In \[\Delta HEG\] , we have,
EG as the base of the \[\Delta HEG\] ,
HJ is the height which is also perpendicular to the base EG.
We know the formula of the area of the triangle,
\[Area=\dfrac{1}{2}\times Base\times Height\]
Now, using this formula to get the area of the \[\Delta HEG\] .
Area of \[\Delta HEG\] = \[\dfrac{1}{2}\times EG\times HJ\] ………………..(2)
We know the property that the distance between parallel lines is always constant. So, each perpendicular distance between the parallel lines is always equal to each other.
Using this property, we can say that,
FI=HJ ………..(3)
From equation (2), and equation (3), we get
Area of \[\Delta HEG\] = \[\dfrac{1}{2}\times EG\times FI\] ………………..(4)
From equation (1), we have
Area of \[\Delta FEG\] = \[\dfrac{1}{2}\times EG\times FI\] .
Now, we can say that equation (1) and equation (4) are equal to each other.
So, Area of \[\Delta HEG\]= Area of \[\Delta FEG\] .
Therefore, two triangles having the same base (or equal bases) have equal areas between the same parallels.
Hence, proved.
Note: In this question, one may think to use heron’s formula for the area of the triangle. That is, \[Area=\sqrt{s\left( s-a \right)\left( s-b \right)\left( s-c \right)}\] . But if we use this formula, then we will not be able to use the property of parallel lines, and also this formula will make our solution complex to solve. Therefore, don’t think to use heron’s formula here.