Question

Prove the following identity \[{{\sin }^{2}}\theta +{{\cos }^{2}}\theta =1\], geometrically.

Answer 1

Hint: To solve this problem use Pythagoras theorem i.e. the square of the hypotenuse of the right angled triangle is equal to the area to the sum of the square on the other two sides.

Let us consider a triangle ABC, where it is right angled at \[{{90}^{\circ }}\] and angle C is taken as \[\theta \].

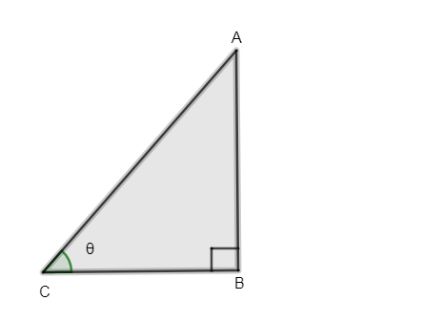
According to angle C \[\theta \], AB is the opposite side, BC is the adjacent side and AC is the hypotenuse.
We know the Pythagoras theorem.
i.e. the square of the hypotenuse of the right angled triangle is equal to the area to the sum of the square on the other two sides.
i.e. \[A{{C}^{2}}=A{{B}^{2}}+B{{C}^{2}}-(1)\]
Now, divide both RHS and LHS with \[A{{C}^{2}}\]
\[\begin{align}
  & \Rightarrow \dfrac{A{{B}^{2}}+B{{C}^{2}}}{A{{C}^{2}}}=\dfrac{A{{C}^{2}}}{A{{C}^{2}}} \\
 & \therefore \dfrac{A{{B}^{2}}}{A{{C}^{2}}}+\dfrac{B{{C}^{2}}}{A{{C}^{2}}}=1\Rightarrow {{\left( \dfrac{AB}{AC} \right)}^{2}}+{{\left( \dfrac{BC}{AC} \right)}^{2}}=1-(2) \\
\end{align}\]
where, \[\dfrac{AB}{AC}=\dfrac{opposite\ side}{hypotenuse}=\sin \theta \]
\[\begin{align}
  & \dfrac{BC}{AC}=\dfrac{adjacent\ side}{hypotenuse}=\cos \theta \\
 & \therefore {{\left( \dfrac{AB}{AC} \right)}^{2}}+{{\left( \dfrac{BC}{AC} \right)}^{2}}=1\Rightarrow {{\left( \sin \theta \right)}^{2}}+{{\left( \cos \theta \right)}^{2}}=1 \\
 & \Rightarrow {{\sin }^{2}}\theta +{{\cos }^{2}}\theta =1 \\
\end{align}\]

Note: This is another method to prove \[{{\sin }^{2}}\theta +{{\cos }^{2}}\theta =1\]

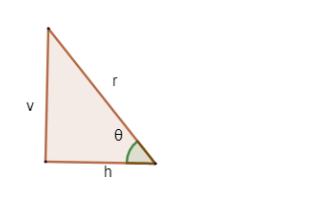
From a right angle triangle, \[\cos \theta =\dfrac{adjacent\ side}{hypotenuse}=\dfrac{h}{r}\]
\[\sin \theta =\dfrac{opposite\ side}{hypotenuse}=\dfrac{v}{r}\]
From Pythagoras theorem, \[{{r}^{2}}={{v}^{2}}+{{h}^{2}}\]
Here, \[\cos \theta =\dfrac{h}{r}\Rightarrow h=r\cos \theta \]
\[\begin{align}
  & \sin \theta =\dfrac{v}{r}\Rightarrow v=r\sin \theta \\
 & \therefore {{r}^{2}}={{\left( r\cos \theta \right)}^{2}}+{{\left( r\sin \theta \right)}^{2}}\Rightarrow {{r}^{2}}={{r}^{2}}{{\cos }^{2}}\theta +{{r}^{2}}{{\sin }^{2}}\theta \\
 & \therefore {{r}^{2}}{{\cos }^{2}}\theta +{{r}^{2}}{{\sin }^{2}}\theta ={{r}^{2}} \\
 & {{r}^{2}}\left( {{\cos }^{2}}\theta +{{\sin }^{2}}\theta \right)={{r}^{2}} \\
 & \Rightarrow {{\cos }^{2}}\theta +{{\sin }^{2}}\theta =1 \\
\end{align}\]