
Prove the identity, $ \sin (A + \pi ) = - \sin A $
Answer
553.8k+ views
Hint: Imagine a unit circle and assume an angle, θ. Mark the corresponding coordinates $ (\cos \theta ,\sin \theta ) $ on the circle. The angle in the question is π more than the unknown angle. In the circle the coordinates corresponding to $ (\pi + \theta ) $ is $ ( - \cos \theta , - \sin \theta ) $ . Thus, we see the sine function for θ has changed to negative sine function upon addition of π.
Complete step-by-step answer:
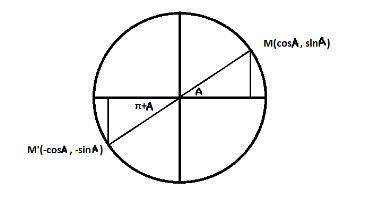
Let us visualize a circle with unit radius and center at origin. Then we mark the angle A on the positive $ (x,y) $ axis. The corresponding point on the circle “M” is $ (\cos A,\sin A) $ . When the angle is changed to $ (\pi + A) $ , the point “M’” has the coordinates $ ( - \cos A, - \sin A) $ as they are located in the III quadrant, i.e., negative x and y axis.
And hence we see, $ \sin (A + \pi ) = - \sin A $ .
Alternate method: Using the identity of summation of angles in the sine function, we can also verify the above asked identity.
We know that, $ \sin (a + b) = \sin a.\cos b + \sin b.\cos a $
Putting $ a = \pi \& b = A $ in the above identity,
$ \sin (\pi + A) = \sin \pi .\cos A + \sin A.\cos \pi \\
Since
\sin \pi = 0 and \cos \pi = -1
we have
$ \sin (A + \pi ) = - \sin A $
Hence, verified.
Note: The functions sine, cosine and tangent of an angle are sometimes remarked as the primary or basic trigonometric functions. The remaining trigonometric functions secant (sec), cosecant (csc), and cotangent (cot) are defined as reciprocals of cosine, sine, and tangent, respectively. Trigonometric identities are equations involving the trigonometric functions that are true for each value of the variables involved.
Complete step-by-step answer:
Let us visualize a circle with unit radius and center at origin. Then we mark the angle A on the positive $ (x,y) $ axis. The corresponding point on the circle “M” is $ (\cos A,\sin A) $ . When the angle is changed to $ (\pi + A) $ , the point “M’” has the coordinates $ ( - \cos A, - \sin A) $ as they are located in the III quadrant, i.e., negative x and y axis.
And hence we see, $ \sin (A + \pi ) = - \sin A $ .

Alternate method: Using the identity of summation of angles in the sine function, we can also verify the above asked identity.
We know that, $ \sin (a + b) = \sin a.\cos b + \sin b.\cos a $
Putting $ a = \pi \& b = A $ in the above identity,
$ \sin (\pi + A) = \sin \pi .\cos A + \sin A.\cos \pi \\
Since
\sin \pi = 0 and \cos \pi = -1
we have
$ \sin (A + \pi ) = - \sin A $
Hence, verified.
Note: The functions sine, cosine and tangent of an angle are sometimes remarked as the primary or basic trigonometric functions. The remaining trigonometric functions secant (sec), cosecant (csc), and cotangent (cot) are defined as reciprocals of cosine, sine, and tangent, respectively. Trigonometric identities are equations involving the trigonometric functions that are true for each value of the variables involved.
Recently Updated Pages
Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Master Class 11 Biology: Engaging Questions & Answers for Success

Trending doubts
One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

There are 720 permutations of the digits 1 2 3 4 5 class 11 maths CBSE

Discuss the various forms of bacteria class 11 biology CBSE

Draw a diagram of a plant cell and label at least eight class 11 biology CBSE

State the laws of reflection of light

Explain zero factorial class 11 maths CBSE




