
Prove work-energy theorem for constant work.
Answer
504.3k+ views
Hint: Work-energy theorem is work on the statement ‘change in energy of the body is equal to work done by the body’. The dimensional of the energy and the work is the same, which also shows that both the quantities are dimensionally equal. So the work and the kinetic energy can be written equal to each other.
Formula Used:
Complete step-by-step solution:
Work-energy theorem: Work-done by a body or work done on a body is equal to change in its kinetic energy.
Assume if the force applied on a body that has mass and due to this force it displaced distance. The initial velocity of the body is
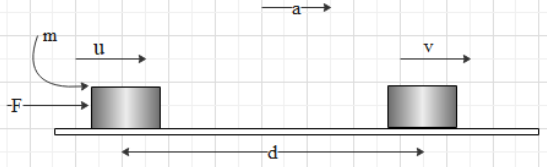
Here the constant force
From the figure,
The well known Newton’s law of motion,
The work done on the body is,
Hence proved that
Note:
(1) Kinetic energy is a scalar quantity. Hence is independent of its path and only depends on the body’s initial velocity magnitude and final velocity magnitude.
(2) The SI unit of work and energy is the same, and it is
(3) The work-energy theorem is the part of the conservation of energy where the potential energy of the body is absent and no external forces (for example friction) present in the motion.
Formula Used:
Complete step-by-step solution:
Work-energy theorem: Work-done by a body or work done on a body is equal to change in its kinetic energy.
Assume if the force applied on a body that has mass and due to this force it displaced distance. The initial velocity of the body is

Here the constant force
From the figure,
The well known Newton’s law of motion,
The work done on the body is,
Hence proved that
Note:
(1) Kinetic energy is a scalar quantity. Hence is independent of its path and only depends on the body’s initial velocity magnitude and final velocity magnitude.
(2) The SI unit of work and energy is the same, and it is
(3) The work-energy theorem is the part of the conservation of energy where the potential energy of the body is absent and no external forces (for example friction) present in the motion.
Recently Updated Pages
Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Trending doubts
Which one is a true fish A Jellyfish B Starfish C Dogfish class 11 biology CBSE

What is the difference between superposition and e class 11 physics CBSE

State and prove Bernoullis theorem class 11 physics CBSE

In which part of the body the blood is purified oxygenation class 11 biology CBSE

1 ton equals to A 100 kg B 1000 kg C 10 kg D 10000 class 11 physics CBSE

State the laws of reflection of light




