Question

What is the radius of curvature of the parabola traced out by the projectile projected at a speed $v$ and projected at an angle \[\theta \] with the horizontal at a point where the particle velocity makes an angle $\dfrac{\theta }{2}$ with the horizontal?
\[
  {\text{A}}{\text{. r = }}\dfrac{{v_{}^2{{\cos }^2}\theta }}{{g{{\cos }^3}\dfrac{\theta }{2}}} \\
    \\
  {\text{B}}{\text{. r = }}\dfrac{{2v\sin \theta }}{{g\tan \theta }} \\
    \\
  {\text{C}}{\text{. r = }}\dfrac{{v\cos \theta }}{{g{{\sin }^2}\dfrac{\theta }{2}}} \\
    \\
  {\text{D}}{\text{. r = }}\dfrac{{3v\cos \theta }}{{g\cot \theta }} \\
 \]

Answer 1

Hint: Here, we can use the formula for velocity and radial acceleration. We know that the velocity is the change in the position of the object with respect to time.
Formula used:
${v_X} = v\cos \theta $
${a_r} = \dfrac{{v_{}^2}}{r}$
Where,
${a_r}$ is the radial acceleration

Complete step-by-step answer:
Let us consider the values given in the above equation.
Given that projectile projected at a speed $v$ and projected at an angle \[\theta \] with the horizontal at a point where the particle velocity makes an angle$\dfrac{\theta }{2}$.
In the diagram the projection of a projectile is shown.

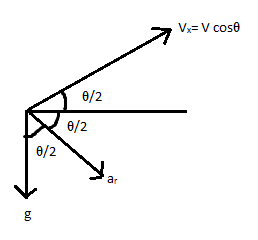
$v$ is the initial speed of the projectile in the horizontal, ${a_r}$ is the radial acceleration acting on the projectile in the direction perpendicular to the direction of initial speed and g is the acceleration due to gravity.

Let us consider the radial acceleration splits into to angles each of $\dfrac{\theta }{2}$.
Let us consider the initial speed of the projectile is in the horizontal direction we have ${v_x} = v\cos \theta $
Also, at a point of interest, the particle velocity makes an angle$\dfrac{\theta }{2}$.
Hence \[v\cos \dfrac{\theta }{2} = v\cos \theta \]
$ \Rightarrow v = \dfrac{{v\cos \theta }}{{\dfrac{{\cos \theta }}{2}}}$
We know that the radial acceleration ${a_r}$is perpendicular to the velocity component as shown in the diagram.
Hence ${a_r} = g\cos \left( {\dfrac{\theta }{2}} \right)$
Velocity in the direction of radial acceleration is given by the relation ${a_r} = \dfrac{{v_{}^2}}{r}$
$ \Rightarrow r = \dfrac{{v_{}^2}}{{{a_r}}}$
Substituting the value,$v = \dfrac{{v\cos \theta }}{{\dfrac{{\cos \theta }}{2}}}$ and ${a_r} = g\cos \left( {\dfrac{\theta }{2}} \right)$ we get,
\[ \Rightarrow r = \dfrac{{\left( {\dfrac{{v_{}^2\cos _{}^2\theta }}{{{{\cos }^2}\dfrac{\theta }{2}}}} \right)}}{{g\cos \dfrac{\theta }{2}}}\]
\[ \Rightarrow r = \dfrac{{v_{}^2\cos _{}^2\theta }}{{{{\cos }^2}\dfrac{\theta }{2} \times g\cos \dfrac{\theta }{2}}}\]
\[ \Rightarrow r = \dfrac{{v_{}^2\cos _{}^2\theta }}{{g{{\cos }^3}\dfrac{\theta }{2}}}\]
Therefore (A) \[r = \dfrac{{v_{}^2\cos _{}^2\theta }}{{g{{\cos }^3}\dfrac{\theta }{2}}}\] is the required answer.
Additional information:
The acceleration of a particle performing uniform circular motion is called radial acceleration.
Radial acceleration is also called centripetal acceleration as it acts along the radius and towards the centre.

Note:let us consider an object that is thrown by the exertion of a force. It is allowed to move freely in the air under the influence of gravity. Therefore, any object that moves through space is called Projectile and the motion is called Projectile motion.