Question

What is the radius of the iodine atom (atomic number is given as $53$, mass number is given as $126$)?
$\begin{align}
  & A.2.5\times {{10}^{-11}}m \\
 & B.2.5\times {{10}^{-9}}m \\
 & C.7\times {{10}^{-9}}m \\
 & D.7\times {{10}^{-6}}m \\
\end{align}$

Answer 1

Hint: The radius of this atom can be found by taking the ratio of the product of the radius of the hydrogen atom and the square of the number of shells of the iodine atom to the atomic number of the iodine atom. The electronic configuration of the atom is to be taken in order to find the number of shells. These all may help you to solve this question.

Complete Answer:
The electronic configuration of the iodine atom can be found at first. The atomic number is given as
$Z=53$
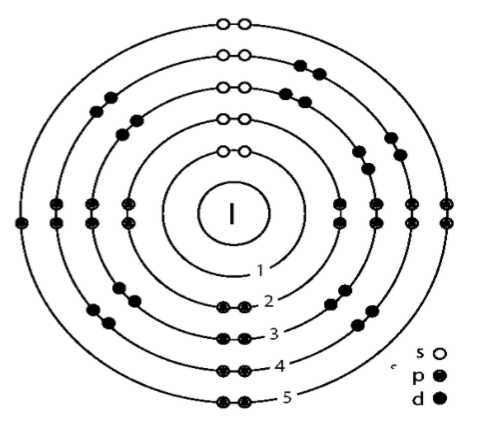
Therefore the electronic configuration will be written as,
$2,8,18,18,7$
From this we can see that the number of shells can be calculated.
That is,
$n=5$
The radius of an atom can be calculated by an equation given as,
${{r}_{n}}={{r}_{H}}\dfrac{{{n}^{2}}}{Z}$
Where ${{r}_{H}}$be the radius of the hydrogen atom, $Z$be the atomic number and $n$ be the number of shells.
The radius of hydrogen atom is given as,
${{r}_{H}}=0.053\times {{10}^{-9}}m$
The atomic number of the iodine atom is given as,
$Z=53$
And the number of shells in the iodine atom is already given as,
\[n=5\]
Substituting the values in it will give,
\[{{r}_{n}}=\left( 0.053\times {{10}^{-9}} \right)\dfrac{{{5}^{2}}}{53}\]
Simplifying the equation will give the radius of iodine atom,
\[{{r}_{n}}=2.5\times {{10}^{-11}}m\]
Therefore the correct answer has been obtained.

The answer is given as option A.

Note:
Iodine is an element in the periodic table which is having the symbol \[I\]. Iodine is helpful in the treatment and prevention of the iodine deficiency and is also used as an antiseptic. Iodine is the least abundant among the halogen gases. And also it is the heaviest mineral nutrient. Radioactive isotopes of the iodine can be used to treat thyroid cancer.