Question

When it is raining vertically downwards, to a man on the road the velocity of rain appears to be 1.5 times his velocity. To protect himself from rain, he should hold the umbrella at an angle \[\theta \] to vertical. Then \[\tan \theta \] is:
A. \[\dfrac{2}{\sqrt{5}}\]
B. \[\dfrac{\sqrt{5}}{2}\]
C. \[\dfrac{2}{3}\]
D. \[\dfrac{3}{2}\]

Answer 1

Hint: In this question, we are asked to calculate the angle at which the man should hold the umbrella to protect himself from rain. We know that velocity is a vector quantity that has magnitude and direction. So, we are basically asked to find the direction of the velocity of rain. We will be using the laws of vector addition to solve this question.

Complete answer:
The velocity of man and velocity of rain are given as shown in the figure below. The given direction of rain is for a man running on the road. Now if the man is made to stand still then the direction of the velocity of rain with respect to man will be given as shown in the figure.

  

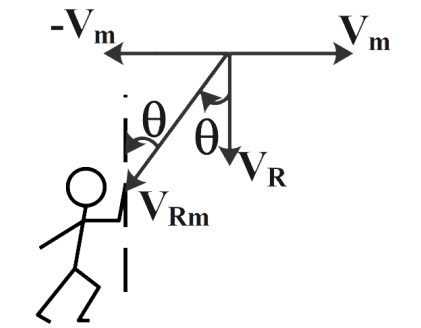
We know that,
\[{{V}_{Rm}}={{V}_{R}}-{{V}_{m}}\]
We also know that
\[{{V}_{Rm}}={{V}_{R}}+(-{{V}_{m}})\]
Therefore, the direction of velocity of rain with respect to man is as shown in the above figure.
Now, it is given that magnitude of velocity of rain with respect to man is equal to 1.5 times the velocity of man
Therefore,
\[\left| {{V}_{Rm}} \right|=1.5\left| {{V}_{m}} \right|\] ………….. (1)
Now, from the above figure, we can say that
\[\sin \theta =\dfrac{\left| {{V}_{m}} \right|}{\left| {{V}_{Rm}} \right|}\]
After substituting the value from (1)
We get,
\[\sin \theta =\dfrac{\left| {{V}_{m}} \right|}{1.5\left| {{V}_{m}} \right|}\]
Therefore,
\[\sin \theta =\dfrac{1}{1.5}=\dfrac{2}{3}\]
Now, from Pythagoras theorem, we know the adjacent side,

                    

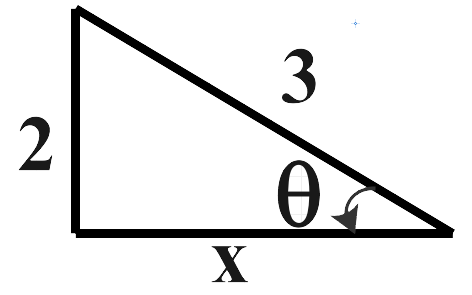
\[{{x}^{2}}=\sqrt{{{3}^{2}}-{{2}^{2}}}\]
Therefore,
\[x=\sqrt{5}\]
Therefore, from trigonometric ratios
We know,
\[\tan \theta =\dfrac{2}{\sqrt{5}}\]

So, the correct answer is “Option A”.

Note:
Problems of this kind are called rain-man problems. These are usually asked in entrance level exams. The easy trick to solve these questions is by using the vector addition and subtraction laws and basic trigonometry. Pythagoras theorem helps us to calculate the third side of a right-angled triangle if the other two sides are known. The modified Pythagoras theorem can help us find out the other sides if one angle and one side is known.