
Reading of ammeter in ampere for the following circuit is:
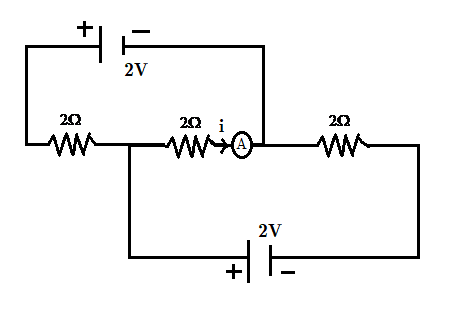
A) \[1\]
B) \[\dfrac{1}{2}\]
C) $\dfrac{2}{3}$
D) $3$
Answer
233.1k+ views
Hint: In the given question, the circuit has two loops. We can apply Kirchhoff’s law for each loop to get the unknown current, voltage or resistance values by using the values given. We need to find the reading of the ammeter in a loop, so we will use the Kirchhoff’s second (voltage) law. As we know, Kirchhoff’s voltage law states that “The voltage around a loop is equal to the sum of every voltage drop in the same loop for any closed circuit”. We will use this law and form the equations for both loops separately and then we can solve the equations to get the value of the unknown parameter.
Complete step by step solution:
We will show the given circuit and name the different parameters in the diagram as shown below:
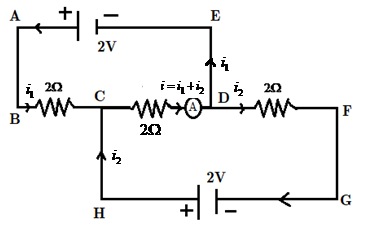
From the circuit, there are two loops i.e. ABCDEA and HCDFGH.
Now, to calculate the unknown parameters, we will use Kirchhoff's voltage law for both loops separately. We will calculate each voltage drop in a loop and put it equal to the voltage in the circuit.
For loop ABCDEA,
\[
\Rightarrow 2{i_1} + 2\left( {{i_1} + {i_2}} \right) = 2 \\
\Rightarrow 2{i_1} + 2{i_1} + 2{i_2} = 2 \\
\Rightarrow 4{i_1} + 2{i_2} = 2 \\
\Rightarrow 2{i_1} + 2{i_2} = 1...\left( 1 \right) \\
\]
For loop HCDFGH,
$
\Rightarrow 2\left( {{i_1} + {i_2}} \right) + 2{i_2} = 2 \\
\Rightarrow 2{i_1} + 2{i_2} + 2{i_2} = 2 \\
\Rightarrow 2{i_1} + 4{i_2} = 2 \\
\Rightarrow {i_1} + 2{i_2} = 1...\left( 2 \right) \\
$
From the equation (1) and (2),
$
\Rightarrow {i_1} + 2\left( {1 - 2{i_1}} \right) = 1 \\
\Rightarrow - 3{i_1} = - 1 \\
\Rightarrow {i_1} = \dfrac{1}{3}A \\
$
On solving,
$
\Rightarrow {i_2} = 1 - 2\left( {\dfrac{1}{3}} \right) \\
\Rightarrow {i_2} = \dfrac{1}{3}A \\
$
Thus, we can calculate the ammeter reading by adding the both currents.
$
i = {i_1} + {i_2} \\
\Rightarrow i = \dfrac{1}{3} + \dfrac{1}{3} \\
\Rightarrow i = \dfrac{2}{3}A \\
$
Therefore, the ammeter reading is $\dfrac{2}{3}A$ .
Hence, the correct option is (C).
Note: In the given question, we need to analyse the circuit and find the law which will help us to find the unknown parameter. For any circuit, we have to look for nodes or loops which are given. After that we can apply Kirchhoff's current law if nodes are given or Kirchhoff’s voltage law if loops are given. The equations for voltage drop and node current will lead us to find the required parameter.
Complete step by step solution:
We will show the given circuit and name the different parameters in the diagram as shown below:

From the circuit, there are two loops i.e. ABCDEA and HCDFGH.
Now, to calculate the unknown parameters, we will use Kirchhoff's voltage law for both loops separately. We will calculate each voltage drop in a loop and put it equal to the voltage in the circuit.
For loop ABCDEA,
\[
\Rightarrow 2{i_1} + 2\left( {{i_1} + {i_2}} \right) = 2 \\
\Rightarrow 2{i_1} + 2{i_1} + 2{i_2} = 2 \\
\Rightarrow 4{i_1} + 2{i_2} = 2 \\
\Rightarrow 2{i_1} + 2{i_2} = 1...\left( 1 \right) \\
\]
For loop HCDFGH,
$
\Rightarrow 2\left( {{i_1} + {i_2}} \right) + 2{i_2} = 2 \\
\Rightarrow 2{i_1} + 2{i_2} + 2{i_2} = 2 \\
\Rightarrow 2{i_1} + 4{i_2} = 2 \\
\Rightarrow {i_1} + 2{i_2} = 1...\left( 2 \right) \\
$
From the equation (1) and (2),
$
\Rightarrow {i_1} + 2\left( {1 - 2{i_1}} \right) = 1 \\
\Rightarrow - 3{i_1} = - 1 \\
\Rightarrow {i_1} = \dfrac{1}{3}A \\
$
On solving,
$
\Rightarrow {i_2} = 1 - 2\left( {\dfrac{1}{3}} \right) \\
\Rightarrow {i_2} = \dfrac{1}{3}A \\
$
Thus, we can calculate the ammeter reading by adding the both currents.
$
i = {i_1} + {i_2} \\
\Rightarrow i = \dfrac{1}{3} + \dfrac{1}{3} \\
\Rightarrow i = \dfrac{2}{3}A \\
$
Therefore, the ammeter reading is $\dfrac{2}{3}A$ .
Hence, the correct option is (C).
Note: In the given question, we need to analyse the circuit and find the law which will help us to find the unknown parameter. For any circuit, we have to look for nodes or loops which are given. After that we can apply Kirchhoff's current law if nodes are given or Kirchhoff’s voltage law if loops are given. The equations for voltage drop and node current will lead us to find the required parameter.
Recently Updated Pages
JEE Main 2026 Session 2 Registration Open, Exam Dates, Syllabus & Eligibility

JEE Main 2023 April 6 Shift 1 Question Paper with Answer Key

JEE Main 2023 April 6 Shift 2 Question Paper with Answer Key

JEE Main 2023 (January 31 Evening Shift) Question Paper with Solutions [PDF]

JEE Main 2023 January 30 Shift 2 Question Paper with Answer Key

JEE Main 2023 January 25 Shift 1 Question Paper with Answer Key

Trending doubts
Why does capacitor block DC and allow AC class 12 physics JEE_Main

Understanding Average and RMS Value in Electrical Circuits

Ideal and Non-Ideal Solutions Explained for Class 12 Chemistry

Understanding Atomic Structure for Beginners

Understanding Elastic Collisions in Two Dimensions

JEE Main Syllabus 2026: Download Detailed Subject-wise PDF

Other Pages
MOSFET: Definition, Working Principle, Types & Applications

Understanding Collisions: Types and Examples for Students

Happy New Year Wishes 2026 – 100+ Messages, Quotes, Shayari, Images & Status in All Languages

Valentine Week 2026 List | Valentine Week Days, Dates & Meaning

One Day International Cricket- India Vs New Zealand Records and Score

Highest T20 Scores in Cricket: Top Records & Stats 2025




