Question

Redefine the function $f(x) = |x - 1| + |x + 1|$. Draw the graph and write its domain and range.

Answer 1

Hint: We will first write down the points where the function can change its values from positive to negative and thus redefine the function using that. Now, after redefining, we will be easily able to draw the graph and thus, we will see the graph and tell about its domain and range.

Complete step-by-step answer:
Let us see the breaking points of the function first. Since, we have the sum of two functions in this function, we will individually see, where the functions take the value 0.
\[\left| {x-1} \right| = 0 \Rightarrow {\text{ }}x = 1\]
\[\left| {x + 1} \right| = 0{\text{ }} \Rightarrow x = - 1\]
Now, we will define the function according to this only.
We know that if we have the function \[p\left( x \right) = \left| x \right|\], then \[p\left( x \right) = \left\{ {\begin{array}{*{20}{c}}
  {x,x > 0} \\
  { - x,x < 0}
\end{array}} \right.\].
Therefore, if \[g\left( x \right) = \left| {x - 1} \right|\], then \[g\left( x \right) = \left\{ {\begin{array}{*{20}{c}}
  {x - 1,x \geqslant 1} \\
  {1 - x,x < 1}
\end{array}} \right.\] ………(1)
And if \[h\left( x \right) = \left| {x + 1} \right|\], then \[h\left( x \right) = \left\{ {\begin{array}{*{20}{c}}
  {x + 1,x \geqslant - 1} \\
  { - (1 + x),x < - 1}
\end{array}} \right.\]. ………….(2)
Now, using (1) and (2), we get all the following result:-
Case I:
Now, if \[x < - 1\], \[g\left( x \right) = \left| {x - 1} \right| = 1 - x\] and \[h\left( x \right) = \left| {x + 1} \right| = - (1 + x)\]
Therefore, when \[x < - 1\], $f(x) = g(x) + h(x) = 1 - x - (1 + x) = 1 - x - 1 - x = - 2x$. ……….(3)
Case II:
Now, when \[ - 1 \leqslant x < 1\], \[g\left( x \right) = \left| {x - 1} \right| = 1 - x\] and \[h\left( x \right) = \left| {x + 1} \right| = 1 + x\]
Therefore, when \[ - 1 \leqslant x < 1\], $f(x) = g(x) + h(x) = 1 - x + 1 + x = 2$. …………..(4)
Case III:
Now, when \[x \geqslant 1\], \[g\left( x \right) = \left| {x - 1} \right| = x - 1\] and \[h\left( x \right) = \left| {x + 1} \right| = 1 + x\]
Therefore, when \[x \geqslant 1\], $f(x) = g(x) + h(x) = x - 1 + 1 + x = 2x$. …………..(5)
Now, using (3), (4) and (5), we get:
$ \Rightarrow f(x) = \left\{ {\begin{array}{*{20}{c}}
  { - 2x,x < - 1} \\
  {2, - 1 \leqslant x < 1} \\
  {2x,x \geqslant 1}
\end{array}} \right.$
Now, we have got an easy redefined function whose graph we can define as follows:-

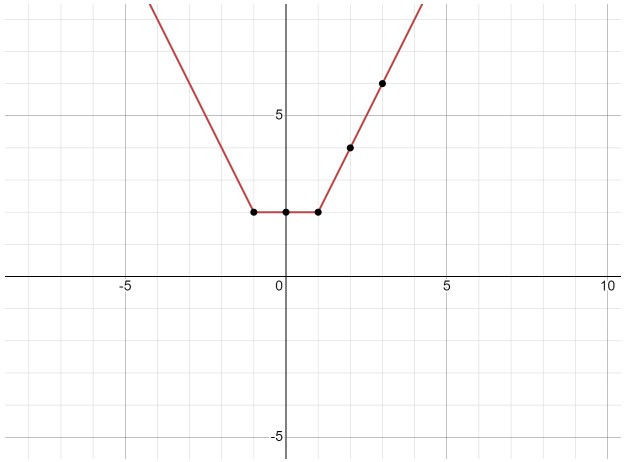
Thus, we have drawn the graph as well.
Now let us talk about the range and domain of the function.
We see that the function is defined for all the real values of $x$. Hence, the domain is the set of real numbers.
Since, we can see that in the output graph, we do not have any values less than 2. Hence, the range will be the set of all real numbers greater than or equal to 2.
Hence, \[Domain = \mathbb{R}\] and \[Range = [2,\infty )\].

Note: The students must know the definition of Domain and Range before answering the questions: Domain is the set of values of $x$ which we can input in the given function without giving rise to any problem and Range is the set of outputs we get after putting in the input.
The students, if not mentioned in the question should still try to make and draw the graph of the function because it helps you see a bigger picture and it will be easy for you to see what domain and range is.