
Regarding the direction of frictional force, which of the following statements is correct?
A. For \[0 \le \theta \le {90^ \circ }\], it always acts leftwards
B. For \[0 \le \theta \le {60^ \circ }\] it acts leftwards and for \[{60^ \circ } \le \theta \le {90^ \circ }\] it acts rightwards
C. It becomes zero at a certain angle \[\theta\] between \[{0^ \circ }\] to \[{90^ \circ }\]
D. None of the above
Answer
383.4k+ views
Hint: When solving questions like these, keep in mind the relationships between angle of friction and angle of repose, and also know how to incorporate those particular concepts into questions. The value of angle of friction depends on the material and nature of surfaces in contact.
Complete step by step solution:
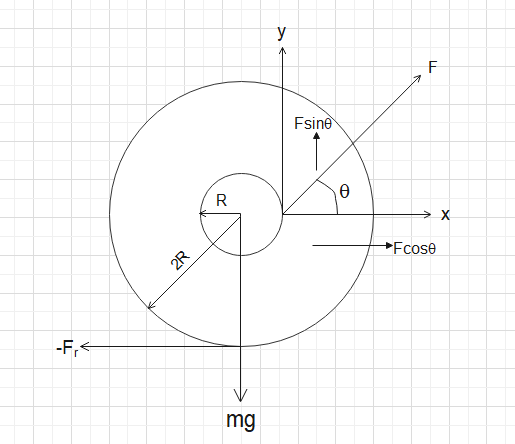
Writing equation of motion (in \[x\] direction)
\[F\cos \theta - {F_r} = ma\] ……(equation 1)
Frictional force is the force that resists motion when a surface of one object comes in contact with the surface of another. Due to friction the output ratio to input ratio is decreased or the mechanical advantage of the machine is sometimes reduced, for which there are provisions made to lessen the friction. There are many types of frictional forces, like static friction, kinetic friction to name a few types.
Torque can be explained as the rotational equivalent of linear force. It is also referred to as moment, moment of force, rotational force, or turning effect. Just as a linear force is a push or pull, a torque can be thought of as a twist to an object around a specific axis. Another way to understand torque can be as a product of magnitude of force and the perpendicular distance of the line of action of a force from the axis of rotation.
Frictional torque is the torque caused by the frictional force that occurs when two objects who are in contact move. Like all other torques, it is a rotational force and can be measured in Newton-metre \[N - m\].
Torque equation for this question can be made as;
\[\Rightarrow \]\[2{F_r}.R(clockwise) + F\cos \theta .R(anticlockwise) + F\sin \theta .R(anticlockwise) = 2m{R^2}\alpha\]
\[\Rightarrow \]\[2{F_r} - F\cos \theta - F\sin \theta = 2m{R^2}\alpha\]
\[\Rightarrow \]\[2{F_r} - F\cos \theta - F\sin \theta = 2ma\] since \[(a = R\alpha )\] ……(2)
Using (equation 1) in (equation 2)
$ \Rightarrow 2(F\cos \theta -ma)-F\cos \theta -F\sin \theta =2ma $
$ \Rightarrow F\cos \theta -F\sin \theta =4ma $
$ \Rightarrow F(\cos \theta -\sin \theta )=4ma $
$ \Rightarrow a=\dfrac{F}{4m(\cos \theta -\sin \theta )} $
$ \Rightarrow F\cos \theta -{{F}_{r}}=\dfrac{mF}{4m(\cos \theta -\sin \theta )} $ Or
$ \Rightarrow F\cos \theta -\dfrac{F}{4(\cos \theta -\sin \theta )}={{F}_{r}} $
$ \Rightarrow {{F}_{r}}=\dfrac{F(4{{\cos }^{2}}\theta -4\sin \theta \cos \theta -1)}{4(\cos \theta -\sin \theta )} $
\[\Rightarrow \]\[{F_r} = \dfrac{F}{4}\dfrac{{(4{{\cos }^2}\theta - 2\sin 2\theta - 1)}}{{(\cos \theta - \sin \theta )}}\]
At \[\theta = {0^ \circ }\] \[{F_r}\] will be maximum.
\[\therefore {{F}_{r}}(\max )=\dfrac{3F}{4}\]
So to conclude we can say that for any angle in between \[{0^ \circ }\] and \[{90^ \circ }\] the direction of frictional force acting against it will be directed leftwards always.
Therefore, the correct answer will be option (A).
Note: Like friction caused by torque, we have other types of friction like fluid friction which is the frictional force that obstructs the flow of fluid. Examples of such friction can be to drop a ball in a bucket full of water, and as a result see water splashing out of the bucket.
Complete step by step solution:

Writing equation of motion (in \[x\] direction)
\[F\cos \theta - {F_r} = ma\] ……(equation 1)
Frictional force is the force that resists motion when a surface of one object comes in contact with the surface of another. Due to friction the output ratio to input ratio is decreased or the mechanical advantage of the machine is sometimes reduced, for which there are provisions made to lessen the friction. There are many types of frictional forces, like static friction, kinetic friction to name a few types.
Torque can be explained as the rotational equivalent of linear force. It is also referred to as moment, moment of force, rotational force, or turning effect. Just as a linear force is a push or pull, a torque can be thought of as a twist to an object around a specific axis. Another way to understand torque can be as a product of magnitude of force and the perpendicular distance of the line of action of a force from the axis of rotation.
Frictional torque is the torque caused by the frictional force that occurs when two objects who are in contact move. Like all other torques, it is a rotational force and can be measured in Newton-metre \[N - m\].
Torque equation for this question can be made as;
\[\Rightarrow \]\[2{F_r}.R(clockwise) + F\cos \theta .R(anticlockwise) + F\sin \theta .R(anticlockwise) = 2m{R^2}\alpha\]
\[\Rightarrow \]\[2{F_r} - F\cos \theta - F\sin \theta = 2m{R^2}\alpha\]
\[\Rightarrow \]\[2{F_r} - F\cos \theta - F\sin \theta = 2ma\] since \[(a = R\alpha )\] ……(2)
Using (equation 1) in (equation 2)
$ \Rightarrow 2(F\cos \theta -ma)-F\cos \theta -F\sin \theta =2ma $
$ \Rightarrow F\cos \theta -F\sin \theta =4ma $
$ \Rightarrow F(\cos \theta -\sin \theta )=4ma $
$ \Rightarrow a=\dfrac{F}{4m(\cos \theta -\sin \theta )} $
$ \Rightarrow F\cos \theta -{{F}_{r}}=\dfrac{mF}{4m(\cos \theta -\sin \theta )} $ Or
$ \Rightarrow F\cos \theta -\dfrac{F}{4(\cos \theta -\sin \theta )}={{F}_{r}} $
$ \Rightarrow {{F}_{r}}=\dfrac{F(4{{\cos }^{2}}\theta -4\sin \theta \cos \theta -1)}{4(\cos \theta -\sin \theta )} $
\[\Rightarrow \]\[{F_r} = \dfrac{F}{4}\dfrac{{(4{{\cos }^2}\theta - 2\sin 2\theta - 1)}}{{(\cos \theta - \sin \theta )}}\]
At \[\theta = {0^ \circ }\] \[{F_r}\] will be maximum.
\[\therefore {{F}_{r}}(\max )=\dfrac{3F}{4}\]
So to conclude we can say that for any angle in between \[{0^ \circ }\] and \[{90^ \circ }\] the direction of frictional force acting against it will be directed leftwards always.
Therefore, the correct answer will be option (A).
Note: Like friction caused by torque, we have other types of friction like fluid friction which is the frictional force that obstructs the flow of fluid. Examples of such friction can be to drop a ball in a bucket full of water, and as a result see water splashing out of the bucket.
Recently Updated Pages
Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Accountancy: Engaging Questions & Answers for Success

The correct geometry and hybridization for XeF4 are class 11 chemistry CBSE

Water softening by Clarks process uses ACalcium bicarbonate class 11 chemistry CBSE

With reference to graphite and diamond which of the class 11 chemistry CBSE

Trending doubts
10 examples of friction in our daily life

Difference Between Prokaryotic Cells and Eukaryotic Cells

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

State and prove Bernoullis theorem class 11 physics CBSE

State the laws of reflection of light

Write down 5 differences between Ntype and Ptype s class 11 physics CBSE




