Question

Represent the following rational numbers on the number line $\dfrac{{ - 7}}{4};\dfrac{4}{{15}}$.

Answer 1

Hint: According to given in the question we have to represent the rational numbers $\dfrac{{ - 7}}{4};\dfrac{4}{{15}}$ on the number line so first of all we have to understand about the rational numbers which is explained as given below:
Rational number: A number that can be obtained by dividing two integers/numbers that can be positive or negative both and the word rational comes from the word ratio or rational numbers are represented in the form $\dfrac{a}{b}$ where the integer b in the denominator should not be zero. It is also a type of a real number so, any fraction with non-zero denominator is a rational number and we can represent it in so many ways as: $\dfrac{1}{2},\dfrac{1}{3},\dfrac{{ - 1}}{2},\dfrac{2}{5},......$
Now, to draw the given rational numbers on the number line first of all we have to understand about number line which is explained below:
Number line: A number line is a representation of numbers on a straight line. With the help of a number line we can compare and order the given numbers that can be any natural number, real number, whole number, prime number, and rational number e.t.c.
So, after drawing the number line we can represent the given rational numbers $\dfrac{{ - 7}}{4};\dfrac{4}{{15}}$ on the number line.

Complete step-by-step answer:
Step 1: First of all we have to draw a number line.

Step 2: Now, as we can see that the rational numbers given in the question are $\dfrac{{ - 7}}{4};\dfrac{4}{{15}}$ so, first of all we will draw $\dfrac{{ - 7}}{4}$on the number line which will lie between -1 and -2 on the number line but in the form of fraction or rational number it will be just between the rational numbers $ - 1.76$and $ - 1.74$
Hence,

Step 3: Now, same as the step 2 we have to draw the given rational number $\dfrac{4}{{15}}$on the number line which will lie between 0 and 1 on the number line but in the form of fraction or rational number it will be just between the rational numbers $0.1$and $0.3$
Hence,

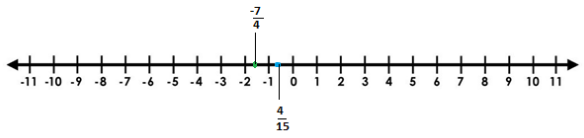
Final solution: Hence, by drawing the number line and placing the given negative and positive rational number we have represented the rational numbers $\dfrac{{ - 7}}{4};\dfrac{4}{{15}}$ on the number line.

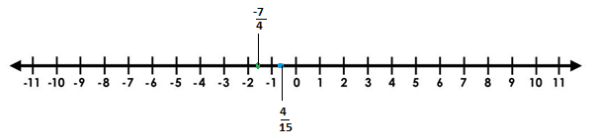
Note: As given in the question rational numbers are $\dfrac{{ - 7}}{4};\dfrac{4}{{15}}$ which will be between the points -1 and -2, 0 and 1 not in between -7 and -8, 4 and 5. So, you have to divide the numerator by denominator to obtain the real exact point.
While representing the points try to divide into 10 subparts that will help you to represent the given number on the number line.