Question

Select incorrect alternative.
A) $ \sin {37^ \circ } = \dfrac{3}{5} $
B) $ \sin {53^ \circ } = \dfrac{4}{5} $
C) $ \tan {37^ \circ } = \dfrac{4}{3} $
D) $ \cos {30^ \circ } = \dfrac{{\sqrt 3 }}{2} $

Answer 1

Hint: Find the incorrect value in the above given trigonometric functions. Use these formulas to find the incorrect one $ \sin \theta = \cos \left( {{{90}^ \circ } - \theta } \right),\tan \theta = \dfrac{{\sin \theta }}{{\cos \theta }} $

Complete step-by-step answer:
We are given four options and we have to find the incorrect one from them.
(A) $ \sin {37^ \circ } = \dfrac{3}{5} $
If a triangle has sides 3, 4, 5 then it is definitely a right angled triangle because the square of 5 is 25 which is equal to square of 3 and 4 which is 16, 9 and one angle of the triangle will be 90 as it is a right triangle and other angles will be 35 and 53 (measure using a protractor).

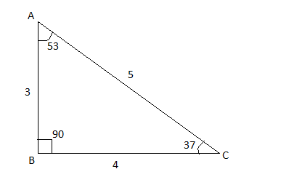
 $ \sin \theta = \dfrac{{opp.side}}{{hypotenuse}} $
Opposite side of angle 37 is AB and hypotenuse is AC
 $
  \sin {37^ \circ } = \dfrac{{AB}}{{AC}} \\
  AB = 3,AC = 5 \\
  \sin {37^ \circ } = \dfrac{3}{5} \\
  $
Therefore, Option A is correct.
(B) $ \sin {53^ \circ } = \dfrac{4}{5} $
We got that $ \sin {37^ \circ } = \dfrac{3}{5} $ from the first option.
We know that $ \sin \theta = \cos \left( {{{90}^ \circ } - \theta } \right) $
So
  $
  \sin {37^ \circ } = \cos \left( {{{90}^ \circ } - {{37}^ \circ }} \right) \\
  \sin {37^ \circ } = \cos {53^ \circ } = \dfrac{3}{5} \\
  $
By Pythagorean trigonometric identity we have $ {\sin ^2}\theta + {\cos ^2}\theta = 1 $
To calculate the value of $ \sin {53^ \circ } $ substitute the value of $ \cos {53^ \circ } $ in the above identity.
 $
  {\sin ^2}{53^ \circ } + {\cos ^2}{53^ \circ } = 1 \\
  \cos {53^ \circ } = \dfrac{3}{5} \\
  {\sin ^2}{53^ \circ } + {\left( {\dfrac{3}{5}} \right)^2} = 1 \\
  {\sin ^2}{53^ \circ } = 1 - {\left( {\dfrac{3}{5}} \right)^2} = 1 - \dfrac{9}{{25}} \\
  {\sin ^2}{53^ \circ } = \dfrac{{25 - 9}}{{25}} = \dfrac{{16}}{{25}} \\
  {\sin ^2}{53^ \circ } = {\left( {\dfrac{4}{5}} \right)^2} \\
  \sin {53^ \circ } = \dfrac{4}{5} \\
  $
Therefore, Option B is also correct.
(C) $ \tan {37^ \circ } = \dfrac{4}{3} $
We know that tangent function is the ratio of sine function and cosine function.
 $ \tan \theta = \dfrac{{\sin \theta }}{{\cos \theta }} $
 $ \tan {37^ \circ } = \dfrac{{\sin {{37}^ \circ }}}{{\cos {{37}^ \circ }}} $
 $ \sin {37^ \circ } = \dfrac{3}{5} $ From the first option.
 $
  \cos \theta = \sin \left( {{{90}^ \circ } - \theta } \right) \\
  \cos {37^ \circ } = \sin \left( {{{90}^ \circ } - {{37}^ \circ }} \right) \\
  \cos {37^ \circ } = \sin \left( {{{53}^ \circ }} \right) \\
  $
 $ \sin {53^ \circ } = \dfrac{4}{5} $ From the second option.
Therefore $ \cos {37^ \circ } = \dfrac{4}{5} $
 $ \tan {37^ \circ } = \dfrac{{\sin {{37}^ \circ }}}{{\cos {{37}^ \circ }}} = \dfrac{{\dfrac{3}{5}}}{{\dfrac{4}{5}}} = \dfrac{3}{4} $
But given that $ \tan {37^ \circ } = \dfrac{4}{3} $ in the first equation which is incorrect.
Therefore Option C is incorrect.
(D) $ \cos {30^ \circ } = \dfrac{{\sqrt 3 }}{2} $

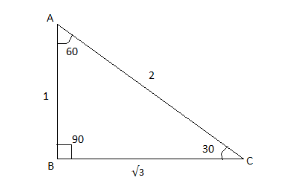
From the triangle, when the sides are 1, √3, 2 then the angles of the triangle are 30, 60, 90.
 $ \cos \theta = \dfrac{{adj.side}}{{hypotenuse}} $
Adjacent side of angle 30 is BC and the hypotenuse is AC.
 $
  \cos {30^ \circ } = \dfrac{{BC}}{{AC}} \\
  \cos {30^ \circ } = \dfrac{{BC}}{{AC}} \\
  BC = \sqrt 3 ,AC = 2 \\
  \cos {30^ \circ } = \dfrac{{\sqrt 3 }}{2} \\
  $
Therefore, Option D is also correct.
Options A, B and D are correct and Option C is incorrect.
So, the correct answer is “Option A,B AND D”.

Note: Trigonometry studies relationships between side lengths and angles. In trigonometry, there are three pairs of co-functions. They are sin-cos, tan-cot, cosec-sec. For these co-functions the value of one co-function of x is equal to the value of other cofunction of 90-x.