Question

Show that a linear combination of sine and cosine function like $x\left( t \right) = a\sin \omega t + b\cos \omega t$ represents a simple harmonic. Also, determine its amplitude and phase constant.

Answer 1

Hint: This question utilizes the concept of harmonic motion and sinusoidal waves. We know that the equation of a SHM is given by $x = A\cos \omega t$ . Thus we need to simplify the above linear equation into \[\cos \] using trigonometric transformations.

Formulae used:
$x = A\cos \omega t$
where $x$ is the displacement of the particle in time $t$ , $\omega $ is the angular frequency and $A$ is the amplitude of the particle.

Complete step by step answer:
The linear combination given to us is,
$x\left( t \right) = a\sin \omega t + b\cos \omega t$ --------------(i)
Now, let us consider a hypothetical triangle $\Delta ABC$ whose perpendicular is $a$ and base is $b$.

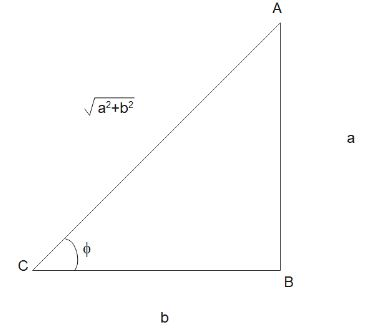
Using Pythagoras theorem, we get the length of the hypotenuse is $\sqrt {{a^2} + {b^2}} $. Now, multiplying and dividing the RHS of eq (i) with $\sqrt {{a^2} + {b^2}} $ , we get
$\Rightarrow x = \dfrac{{\sqrt {{a^2} + {b^2}} }}{{\sqrt {{a^2} + {b^2}} }}\left( {a\sin \omega t + b\cos \omega t} \right) \\
\Rightarrow x = \sqrt {{a^2} + {b^2}} \left( {\dfrac{a}{{\sqrt {{a^2} + {b^2}} }}\sin \omega t + \dfrac{b}{{\sqrt {{a^2} + {b^2}} }}\cos \omega t} \right) \\$ --------------(ii)
Now, from the triangle, we know that $\sin \phi = \dfrac{a}{{\sqrt {{a^2} + {b^2}} }}$ and $\cos \phi = \dfrac{b}{{\sqrt {{a^2} + {b^2}} }}$
Substituting these values in equation (ii), we get
$\Rightarrow x = \sqrt {{a^2} + {b^2}} \left( {\sin \phi \sin \omega t + \cos \phi \cos \omega t} \right) \\
\Rightarrow x = \sqrt {{a^2} + {b^2}} \left( {\cos \omega t\cos \phi + \sin \omega t\sin \phi } \right) $
Using the trigonometric transformation $\cos \left( {A - B} \right) = \cos A\cos B + \sin A\sin B$ , we get
$ \Rightarrow x = \sqrt {{a^2} + {b^2}} \cos \left( {\omega t - \phi } \right)$ ---------------(iii)
This equation resembles that of a SHM. Here, its amplitude is $\sqrt {{a^2} + {b^2}} $ and its phase constant is $\phi $

Now, to find the value of its phase constant, we have
$\Rightarrow \tan \phi = \dfrac{{\sin \phi }}{{\cos \phi }} \\
\Rightarrow \tan \phi = \dfrac{{\dfrac{a}{{\sqrt {{a^2} + {b^2}} }}}}{{\dfrac{b}{{\sqrt {{a^2} + {b^2}} }}}} \\
\Rightarrow \tan \phi = \dfrac{a}{b} \\
\therefore \phi = {\tan ^{ - 1}}\dfrac{a}{b} $
We know from eq (iii) that the value of $\phi $ is negative.

Thus the phase constant is $ - {\tan ^{ - 1}}\dfrac{a}{b}$.

Note: We could have also solved the question by taking $a$ as base and $b$ as perpendicular. By doing that, we would have got the equation as $x = \sqrt {{a^2} + {b^2}} \sin (\omega t + \phi )$ . Then, using trigonometric transformations to convert sine to cosine, we would have again reached the same answer with different phase constant.