Question

Show that a median of a triangle divides it into two triangles of equal area.

Answer 1

Hint: To prove, we draw a median to the given triangle. We use the definition of median. Then we’ll have two triangles with a common vertex and bases of equal length. Find the area of one triangle and show it is equal to the other.

Complete Step-by-Step solution:

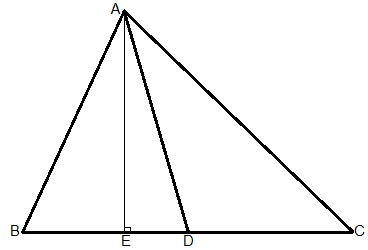
Let ABC be a triangle.
Let AD be one of its medians.

∆ABD and ∆ADC have the vertex A in common.

Hence, the bases BD and DC are equal (as AD is the median).

Now, draw a line AE perpendicular to BC, AE ⊥ BC.

We know the area of a triangle with base b and height h is = $\dfrac{1}{2} \times {\text{b}} \times {\text{h}}$

Now area of triangle ∆ABD = $\dfrac{1}{2} \times {\text{base}}$× altitude of ∆ABD
                                           = $\dfrac{1}{2} \times {\text{BD}} \times {\text{AE}}$
                                 = $\dfrac{1}{2} \times {\text{DC}} \times {\text{AE}}$ --- (Since BD = DC)

But DC and AE are the base and altitude of ∆ACD respectively.

Area of ∆ACD = $\dfrac{1}{2}$× base DC × altitude of ∆ACD
                           = $\dfrac{1}{2} \times {\text{DC}} \times {\text{AE}}$

Hence, area of (∆ABD) = area of (∆ACD)
Hence the median of a triangle divides it into two triangles of equal areas.

Note – The key in such problems is to draw a figure and include a median in it. This makes the figure into two triangles with a common vertex and equal bases.
Finding the area of one triangle and using the condition of equal bases gives us the proof.
(In geometry, a median of a triangle is a line segment joining a vertex to the midpoint of the opposite side, thus bisecting that side.)