Question

Show that every equiangular triangle is equilateral.

Answer 1

Hint: Firstly, we will construct a triangle whose angle equals to ${{60}^{\circ }}$ . after that, in triangle ABC, using the property of triangle which states that sides opposites to equal angles are equal, we will show that pairs of sides of the triangle are equal. Hence, we will show that ABC is an equilateral triangle.

Complete step-by-step solution:
Let, there be triangle ABC whose angles are equal to ${{60}^{\circ }}$.

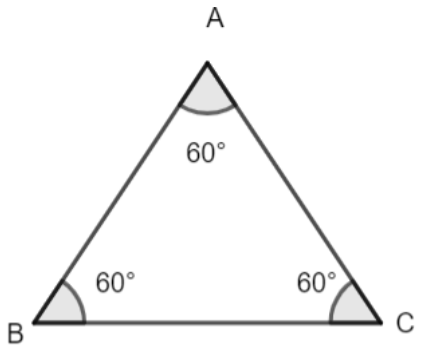
Now, in triangle ABC, we have
$\angle B=\angle C$, as given in the question.
We know that there is a proven statement for general triangles that sides opposite to equal angles are also equal.
As the side opposite to $\angle B$ is AC and the side opposite to $\angle C$ is AB.
Then, we can say that
$AC = AB$.............( i )
Similarly, we can see from the figure that,
$\angle A=\angle C$
As the side opposite to $\angle A$ is BC and the side opposite to $\angle C$ is AB.
Using the same statement we used for the above equation, we can say that
$BC = AB$ …………..( ii )
From equation ( i ) and equation ( ii ), we can say that
$AB = BC = AC$
Also, we know that all sides of the equilateral triangle are equal.
Hence, we can say that every equiangular triangle is equilateral.

Note: Always remember that equiangular means angles of the same measure of a polygon. Also, vice versa of statement sides opposite to equal angles are also equal is true. To prove for all sides of the triangle equal, we need to prove at least two pairs of sides equal. Do not forget to draw a diagram and label it correctly.