Question

Show that if the diagonals of a quadrilateral bisect each other at right angles, then it is a rhombus.

Answer 1

Hint: Let us suppose a quadrilateral ABCD with two diagonals bisect each other at ${{90}^{\circ }}$. We know that there is a property of a rhombus that all of its sides are equal so if we prove that all of the sides of the quadrilateral ABCD are equal then we can show that the quadrilateral is a rhombus.

Complete step-by-step solution:
In the below diagram, we have shown a quadrilateral ABCD with the diagonals intersect each other at point O.

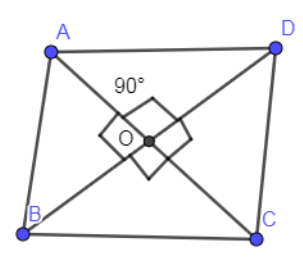
Let us assume the length of diagonals AC as “p” and BD as “q” in the above diagram.
Now, as diagonals bisect each other so:
$\begin{align}
  & AO=OC=\dfrac{p}{2} \\
 & BO=OD=\dfrac{q}{2} \\
\end{align}$
Now, we are going to find the lengths of the sides of the quadrilateral ABCD.
The diagonals cut the quadrilateral in 4 right-angled triangles so applying Pythagoras theorem in the right triangles.
In Pythagoras theorem,
${{\left( Hypotenuse \right)}^{2}}={{\left( base \right)}^{2}}+{{\left( perpendicular \right)}^{2}}$
In $\Delta AOD$, applying Pythagoras theorem we get,
${{\left( AD \right)}^{2}}={{\left( AO \right)}^{2}}+{{\left( OD \right)}^{2}}$
Substituting AO as $\dfrac{p}{2}$ and OD as $\dfrac{q}{2}$ in the above equation we get,
$\begin{align}
  & {{\left( AD \right)}^{2}}={{\left( AO \right)}^{2}}+{{\left( OD \right)}^{2}} \\
 & \Rightarrow {{\left( AD \right)}^{2}}={{\left( \dfrac{p}{2} \right)}^{2}}+{{\left( \dfrac{q}{2} \right)}^{2}} \\
\end{align}$
Taking square root on both the sides we get,
$\begin{align}
  & \left( AD \right)=\sqrt{\dfrac{{{p}^{2}}}{4}+\dfrac{{{q}^{2}}}{4}} \\
 & \Rightarrow \left( AD \right)=\dfrac{\sqrt{{{p}^{2}}+{{q}^{2}}}}{2} \\
\end{align}$
Applying Pythagoras theorem in $\Delta AOB$ we get,
${{\left( AB \right)}^{2}}={{\left( AO \right)}^{2}}+{{\left( OB \right)}^{2}}$
Substituting AO as $\dfrac{p}{2}$ and OB as $\dfrac{q}{2}$ we get,
${{\left( AB \right)}^{2}}={{\left( \dfrac{p}{2} \right)}^{2}}+{{\left( \dfrac{q}{2} \right)}^{2}}$
Taking square root on both the sides we get,
$\begin{align}
  & \left( AB \right)=\sqrt{\dfrac{{{p}^{2}}}{4}+\dfrac{{{q}^{2}}}{4}} \\
 & \Rightarrow \left( AB \right)=\dfrac{\sqrt{{{p}^{2}}+{{q}^{2}}}}{2} \\
\end{align}$
Applying Pythagoras theorem in $\Delta BOC$ we get,
${{\left( BC \right)}^{2}}={{\left( BO \right)}^{2}}+{{\left( OC \right)}^{2}}$
Substituting OC as $\dfrac{p}{2}$ and BO as $\dfrac{q}{2}$ we get,
${{\left( BC \right)}^{2}}={{\left( \dfrac{q}{2} \right)}^{2}}+{{\left( \dfrac{p}{2} \right)}^{2}}$
Taking square root on both the sides we get,
$\begin{align}
  & \left( BC \right)=\sqrt{\dfrac{{{q}^{2}}}{4}+\dfrac{{{p}^{2}}}{4}} \\
 & \Rightarrow \left( BC \right)=\dfrac{\sqrt{{{p}^{2}}+{{q}^{2}}}}{2} \\
\end{align}$
Applying Pythagoras theorem in $\Delta COD$ we get,
${{\left( CD \right)}^{2}}={{\left( CO \right)}^{2}}+{{\left( OD \right)}^{2}}$
Substituting CO as $\dfrac{p}{2}$ and OD as $\dfrac{q}{2}$ we get,
${{\left( CD \right)}^{2}}={{\left( \dfrac{p}{2} \right)}^{2}}+{{\left( \dfrac{q}{2} \right)}^{2}}$
Taking square root on both the sides we get,
$\begin{align}
  & \left( CD \right)=\sqrt{\dfrac{{{p}^{2}}}{4}+\dfrac{{{q}^{2}}}{4}} \\
 & \Rightarrow \left( CD \right)=\dfrac{\sqrt{{{p}^{2}}+{{q}^{2}}}}{2} \\
\end{align}$
From the above calculations, you can see that all the sides AB, BC, CD and AD are of same length i.e. $\dfrac{\sqrt{{{p}^{2}}+{{q}^{2}}}}{2}$.
As we have proved that all the sides are equal so the property of rhombus that all the sides are equal is satisfying.
Hence, we have shown that when diagonals of the quadrilateral bisect each other at right angles then the quadrilateral is a rhombus.

Note: The point to be noted is that all the sides are equal and diagonals bisect each other at right angles are also the properties of a square so you might think it could be a square too. Yeah, it can be but there is no information about the internal angles of the quadrilateral given and additionally, the question is asking us to show that the quadrilateral is a rhombus so we haven’t discussed anything about the square in the above solution.