Question

Show that Kinetic energy is always lost in inelastic collisions.

Answer 1

Hint: In order to solve this question, we should know that inelastic collisions are predefined as those collisions in which momentum remain conserved but kinetic energy lost in form of heat, sound and other forms of energy, here we will understand the perfectly inelastic collision and will figure out the lost in kinetic energy of the system.

Complete step by step answer:
A perfectly inelastic collision is one in which after the collision both the colliding bodies stick together and move with same velocity. Let us suppose two bodies having mass of ${m_1},{m_2}$ and ${m_1}$ is moving with velocity ${v_1}$ while ${m_2}$ is at rest initially before the collision. So, the initial momentum of the system will be ${P_i} = {m_1}{v_1}$.

Now, let us suppose both bodies collide and stick together and moves with same velocity say v’ then, final mass of the system will be $({m_1} + {m_2})$ so, final momentum of this system after the collision will be ${P_f} = ({m_1} + {m_2})v'$ as shown in the diagram,

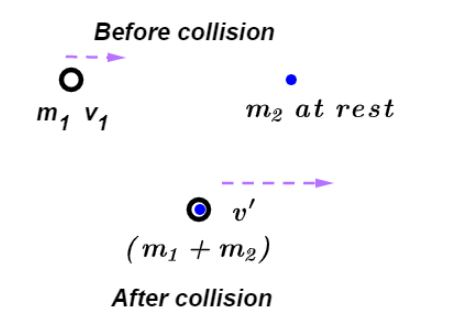
Now, initial momentum will be equal to that of final momentum according to law of conservation of linear momentum so, equation initial and final momentum we get,
${P_i} = {P_f}$ putting values we get,
$\Rightarrow {m_1}{v_1} = ({m_1} + {m_2})v' \to (i)$
Now, let initial kinetic energy of the system be $K{E_i}$ then it will be given by
$K{E_i} = \dfrac{1}{2}{m_1}{v_1}^2$ and final kinetic energy $K{E_f}$ will be given by,
$\Rightarrow K{E_f} = \dfrac{1}{2}({m_1} + {m_2})v{'^2}$
from equation (i) put the value of $v' = \dfrac{{{m_1}{v_1}}}{{({m_1} + {m_2})}}$ in above equation, we get
$K{E_f} = \dfrac{1}{2}({m_1} + {m_2}){[\dfrac{{{m_1}{v_1}}}{{({m_1} + {m_2})}}]^2}$ on simplifying we can write it as,
$\Rightarrow K{E_f} = \dfrac{1}{2}\dfrac{{{{({m_1}{v_1})}^2}}}{{({m_1} + {m_2})}}$

Now, let us find the value of $\text{Loss} = K{E_i} - K{E_f}$ which is loss in kinetic energy, hence on putting the value of parameters we get,
$\Rightarrow \text{Loss} = \dfrac{1}{2}{m_1}{v_1}^2 - \dfrac{1}{2}\dfrac{{{{({m_1}{v_1})}^2}}}{{({m_1} + {m_2})}}$
$\Rightarrow \text{Loss} = \dfrac{1}{2}{m_1}{v_1}^2[1 - \dfrac{{{m_1}}}{{{m_1} + {m_2}}}]$
$\therefore \text{Loss} = \dfrac{1}{2}{m_1}{v_1}^2[\dfrac{{{m_2}}}{{{m_1} + {m_2}}}]$

Hence, there is non-zero value in difference between initial kinetic energy and final kinetic energy which shows that, Kinetic energy is always lost in inelastic collision and this loss has a magnitude of $\text{Loss} = \dfrac{1}{2}{m_1}{v_1}^2[\dfrac{{{m_2}}}{{{m_1} + {m_2}}}]$.

Note: It should be remembered that, when two bodies stick together their mass will be a combined sum of mass of individual bodies and they will together move with same velocity and this is called a perfectly inelastic collision. while in elastic collision initial kinetic energy and final kinetic energy are always equal.