Question

Show that the angle bisectors of a parallelogram form a rectangle.

Answer 1

Hint: To prove that the angle bisector of a parallelogram form a rectangle we have to prove that the interior angle of the quadrilateral formed by the angle bisector are right angle. Then the quadrilateral will be a rectangle

Complete step-by-step answer:
Suppose the diagram of the parallelogram is as the figure given below.

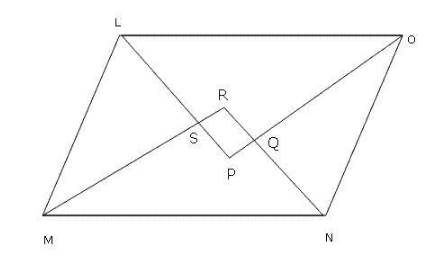
LMNO is a parallelogram in which bisectors of the angles L, M, N, and O intersect at P, Q, R and S to form the quadrilateral PQRS.
 \[LM{\text{ }}||{\text{ }}NO\;\] (opposite sides of parallelogram LMNO)
$\angle L + \angle M = 180^\circ $ (sum of consecutive interior angles is 180o)
 \[\angle MLS{\text{ }} + \;\angle LMS{\text{ }} = {90^o}\]
In \[\Delta LMS,\;\;\angle MLS{\text{ }} + \;\angle LMS{\text{ }} + \;\angle LSM{\text{ }} = {180^o}\]
 \[{90^o}\; + \;\angle LSM{\text{ }} = {\text{ }}180^\circ \]
 \[\angle LSM{\text{ }} = {\text{ }}{90^o}\]
Hence, \[\angle RSP{\text{ }} = {\text{ }}{90^o}\] , (vertically opposite angles)
Similarly, \[\angle SRQ{\text{ }} = {\text{ }}{90^o},\;{\text{ }}\angle RQP{\text{ }} = {\text{ }}{90^o}\;\] and \[\angle SPQ{\text{ }} = {\text{ }}{90^o}\]
Hence the angle bisectors of a parallelogram form a rectangle as all the angles are right angles; we conclude that it IS RECTANGLE.
Hence proved.

Note: A rectangle is a kind of regular geometry in which the length of opposite sides are equal and all the interior angles are right angles. It differs from that of square in only one sense that in square all the four sides are equal.