
Show that the area of the rhombus is half the product of the lengths of its diagonals.
Answer
495.9k+ views
Hint: In this question, we need to prove that the area of the rhombus is half the product of the lengths of its diagonals. For this, we will use the geometrical, mathematical formulae along with the properties of the rhombus.
Complete step-by-step answer:
Let ABCD be a rhombus with AC and BD as the diagonals with the length
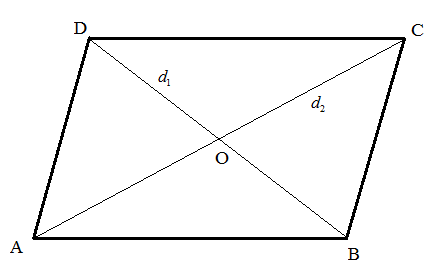
As the diagonals of the rhombus bisect each other at 90 degrees. So, the following figure has been generated.
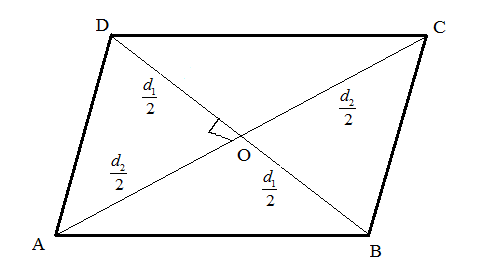
From the above figure, we can write that the area of the rhombus ABCD has been divided into the area of the triangles ABC and ADC.
Now, the triangles ABC and ADC are two right-angled triangles with BO perpendicular to AC and DO perpendicular to AC.
Half of the product of the base and the height of a triangle is the area of the triangle. Mathematically,
So, the area of the triangle ABC is given as
Similarly, the area of the triangle ADC is given as
As, the sum of the areas of the triangles ABC and ADC is equal to the area of the rhombus ABCD. Mathematically,
Substituting the values of the areas of the triangles in the equation
From the figure, we can see that the sum of BO and DO is equalled to the length of the diagonal BD. So, substituting (BO+DO=BD) in the equation (iii), we get
Also, from the figure, we can see that the length of the diagonal AC is
Hence, we can say that the area of the rhombus is half of the product of the length of the diagonals.
Note: Students must note that the length of the diagonals in a rhombus are different and they bisect each other at 90 degrees. Moreover, rhombus differs from the square in one thing only that the length of the diagonals in the square are the same.
Complete step-by-step answer:
Let ABCD be a rhombus with AC and BD as the diagonals with the length

As the diagonals of the rhombus bisect each other at 90 degrees. So, the following figure has been generated.

From the above figure, we can write that the area of the rhombus ABCD has been divided into the area of the triangles ABC and ADC.
Now, the triangles ABC and ADC are two right-angled triangles with BO perpendicular to AC and DO perpendicular to AC.
Half of the product of the base and the height of a triangle is the area of the triangle. Mathematically,
So, the area of the triangle ABC is given as
Similarly, the area of the triangle ADC is given as
As, the sum of the areas of the triangles ABC and ADC is equal to the area of the rhombus ABCD. Mathematically,
Substituting the values of the areas of the triangles in the equation
From the figure, we can see that the sum of BO and DO is equalled to the length of the diagonal BD. So, substituting (BO+DO=BD) in the equation (iii), we get
Also, from the figure, we can see that the length of the diagonal AC is
Hence, we can say that the area of the rhombus is half of the product of the length of the diagonals.
Note: Students must note that the length of the diagonals in a rhombus are different and they bisect each other at 90 degrees. Moreover, rhombus differs from the square in one thing only that the length of the diagonals in the square are the same.
Recently Updated Pages
Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Questions & Answers - Ask your doubts

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Master Class 11 Science: Engaging Questions & Answers for Success

Trending doubts
List some examples of Rabi and Kharif crops class 8 biology CBSE

Write five sentences about Earth class 8 biology CBSE

Summary of the poem Where the Mind is Without Fear class 8 english CBSE

How many ten lakhs are in one crore-class-8-maths-CBSE

Advantages and disadvantages of science

In a school there are two sections of class X section class 8 maths CBSE




