Question

Show that the difference between any two sides of a triangle is less than the third side.

Answer 1

Hint: We solve this problem by constructing an isosceles triangle within the general triangle that is as shown below.
 

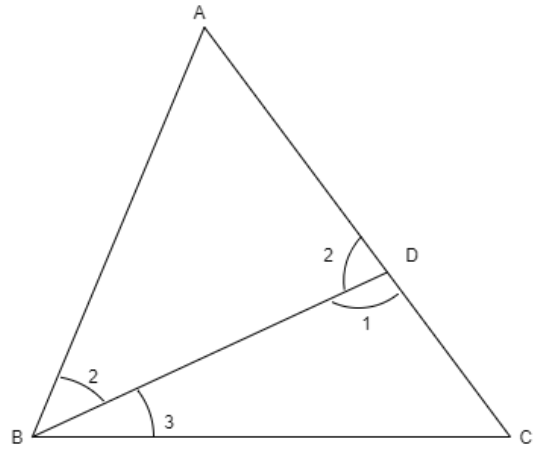
Here, \[AB=AD\] we know that the angles opposite to equal sides are equal and the exterior angle is equal to the sum of opposite two angles. By using these two theorems we need to prove \[DC< BC\] which gives the required result.

Complete step-by-step solution:
Let us consider a triangle \[\Delta ABC\]
Now, let us construct the side \[BD\] such that \[AB=AD\] as shown below

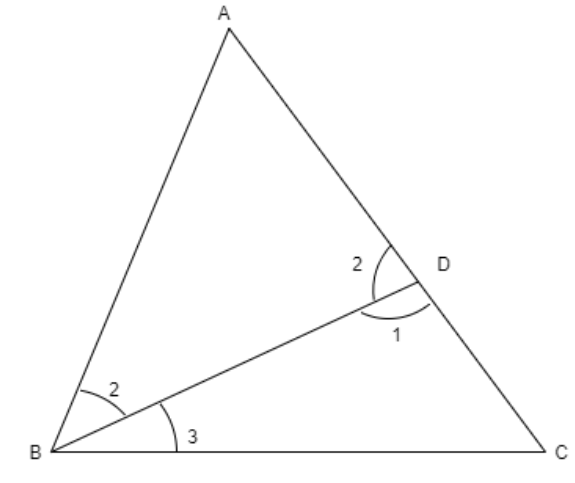
We know that the angles opposite to equal sides are equal.
By using the above theorem we can write
\[\angle ABD=\angle ADB=\angle 2\]
We know that the exterior angle is equal to the sum of the opposite angles.
By using the above theorem we can write
\[\begin{align}
  & \Rightarrow \angle BDC=\angle A+\angle ABD \\
 & \Rightarrow \angle 1=\angle A+\angle 2 \\
\end{align}\]
Here, we can see that we need to add \[\angle A\] to \[\angle 2\] for getting \[\angle 1\]
So, from the inequality we can write
\[\Rightarrow \angle 1> \angle 2.....equation(i)\]
 Now, similarly let us go for \[\Delta DBC\] that is
\[\begin{align}
  & \Rightarrow \angle ADB=\angle C+\angle DBC \\
 & \Rightarrow \angle 2=\angle C+\angle 3 \\
\end{align}\]
Here, we can see that we need to add \[\angle C\] to \[\angle 3\] for getting \[\angle 2\]
So, from the inequality we can write
\[\Rightarrow \angle 2 >\angle 3.....equation(ii)\]
Now, by combining the equation (i) and equation (ii) we get
\[\begin{align}
  & \Rightarrow \angle 1> \angle 2> \angle 3 \\
 & \Rightarrow \angle 1> \angle 3 \\
 & \Rightarrow \angle 3<\angle 1 \\
\end{align}\]
We know that we can replace the sides in an inequality with their opposite angles and vice versa.
By using the above theorem we can take the sides opposite to \[\angle 3\] and \[\angle 1\] from \[\Delta DBC\] to get
\[\begin{align}
  & \Rightarrow \angle 3< \angle 1 \\
 & \Rightarrow DC< BC \\
\end{align}\]
Here, we have the length \[DC\] can be written as
\[\Rightarrow AC-AD< BC\]
Now, by substituting \[AB=AD\] in above equation we get
\[\Rightarrow AC-AB< BC\]
Therefore, we can see that the difference of two sides is less than the third side.
Hence the required result has been proved.

Note: The explanation for the above question can be done in another way also.
We know that the definition of a triangle as the polygon having three sides such that the sum of any two sides is greater than the third side.
Let us consider a triangle \[\Delta ABC\]

From the definition of triangle, we can write
\[\Rightarrow AB+BC>AC\]
Now, the above equation can be reformed as
\[\Rightarrow AC-BC< AB\]
Therefore, we can say that the difference between two sides is less than the third side.
Similarly, we can say for all sides.